Question 379792: solve the equation exactly in the complex number system 7x^3+3x^2-29x+11=0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
To solve this we need to factor it. The Greatest Common Factor (GCF) is 1 (which we do not usually bother factoring out. The expression has 4 terms which is too many for factoring by patterns or trinomial factoring. All we have left is factoring by grouping or factoring by trial and error of the possible rational roots. I don't see how to use factoring by grouping so we will try the rational roots.
The possible rational roots of a polynomial are all the ratios/fractions, positive and negative, which can be formed with a factor of the constant term (at the end) in the numerator and a factor of the leading coefficient (in front of the highest power term).
So the possible rational roots of your polynomial are 1/1, -1/1, 11/1, -11/1, 1/7, -1/7, 11/7, -11/7. The first two, 1 and -1, are possible rational roots of all polynomials since 1 is a factor of everything. They are also easy to check since powers of 1 are extremely easy and powers of -1 just a little bit harder. A quick check will show that neither of these work. For the other rational roots, the quickest way to check, IMHO, is to use synthetic division. To save time I am going to go directly to the rational root that works:
11/7 | 7 3 -29 11
------ 11 22 -11
-----------------
7 14 -7 0
The zero in the lower right corner tells us that (x-11/7) divides evenly into the polynomial. And if it divides evenly the it is a factor of the polynomial. And if (x-11/7) is a factor then, when x = 11/7 the factor is zero. And if the factor is zero the product will be zero. This makes 11/7 one of the solutions to the equation.
Not only that, the rest of the bottom line tells us the other factor. The "7 14 -7" tells us that the other factor is 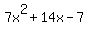 is the other factor. This other factor is a quadratic expression. We can factor out a 7 giving: is the other factor. This other factor is a quadratic expression. We can factor out a 7 giving: 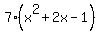 . The remaining quadratic does not factor easily but we can use the Quadratic Formula: . The remaining quadratic does not factor easily but we can use the Quadratic Formula:

which simplifies as follows:










This makes three solutions to the equation:



|
|
|