|
Question 379778: Given: x^2 - y^2 = 8x -2y -13. Find the center, the vertices, the foci, and the asymptotes. Then draw the graph neatly, please.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given:  . Find the center, the vertices, the foci, and the asymptotes. Then draw the graph neatly, please . Find the center, the vertices, the foci, and the asymptotes. Then draw the graph neatly, please
This is a hyperbola because the  and the and the  term have opposite
signs. term have opposite
signs.
 Get it like this:
Get it like this:
 Put parentheses around the first two terms:
Put parentheses around the first two terms:
 Factor -1 out of the last two terms on the left
Factor -1 out of the last two terms on the left
 Take half of -8, get -4, square it get +16, add +16 inside the
first parentheses and add +16 to the right side:
Take half of -8, get -4, square it get +16, add +16 inside the
first parentheses and add +16 to the right side:
 Take half of -2, get -1, square it get +1, add +1 inside the second
parentheses, but because of the - in front of the second parentheses
on the left we add -1 to the right side:
Take half of -2, get -1, square it get +1, add +1 inside the second
parentheses, but because of the - in front of the second parentheses
on the left we add -1 to the right side:
 Factor the two parentheses as perfect squares, Combine the terms on the
right.
Factor the two parentheses as perfect squares, Combine the terms on the
right.
 Get a 1 on the right side by dividing every term through by 2
Get a 1 on the right side by dividing every term through by 2

 Compare that to
Compare that to
 and since the term in x is the positive one, we know the hyperbola
opens right and left. (As we know the x-axis goes right and left, a
way to remember it).
Comparing further, center = (h,k) = (4,1)
We plot the center
and since the term in x is the positive one, we know the hyperbola
opens right and left. (As we know the x-axis goes right and left, a
way to remember it).
Comparing further, center = (h,k) = (4,1)
We plot the center
 Comparing further:
Comparing further:
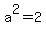 so so  Length of semi-transverse axis = a =
Length of semi-transverse axis = a =  So we draw the transverse axis
So we draw the transverse axis  about 1.4 units
to the right and to the left of the center: about 1.4 units
to the right and to the left of the center:
 The ends of the transverse axis are the vertices. We subtract "a"
from "h" to get the x-coordinate of the left vertex, so the left
vertex is
(4-
The ends of the transverse axis are the vertices. We subtract "a"
from "h" to get the x-coordinate of the left vertex, so the left
vertex is
(4- ,1).
We add "a" to "h" to get the x-coordinate of the right vertex, so
the right vertex is V(4+ ,1).
We add "a" to "h" to get the x-coordinate of the right vertex, so
the right vertex is V(4+ ,1). They have the same
y-coordinate as the center. ,1). They have the same
y-coordinate as the center.
 so so  Length of semi-conjugate axis = b =
Length of semi-conjugate axis = b =  So we draw the conjugate axis
So we draw the conjugate axis  about 1.4 units
above and below the center: about 1.4 units
above and below the center:
 Next we draw the defining rectangle around the two axes:
Next we draw the defining rectangle around the two axes:
 We draw the asymptotes by drawing the extended diagonals of the
defining rectangle:
We draw the asymptotes by drawing the extended diagonals of the
defining rectangle:
 These asymptotes have slopes
These asymptotes have slopes  The go through the center (4,1) so their equations are gotten using
the point-slope formula:
The go through the center (4,1) so their equations are gotten using
the point-slope formula:
 Finding the equation of the asymptote with the positive slope
Finding the equation of the asymptote with the positive slope


 Finding the equation of the asymptote with the begative slope
Finding the equation of the asymptote with the begative slope


 Finally we sketch in the hyperbola:
Finally we sketch in the hyperbola:
 Edwin
Edwin
|
|
|
| |