Question 378815: Hi I am studting logarithms today with an exam tommorow.Unfortunatly i missed the logarithms lecture as i was sick so I am finding it hard to to solve some of the problems.would really appreciate some help solving these step by step so i can understand it better.



i know iv put up 3 so this might be too muych so if you can only help me solve 1 i would appreciate that too.thanks in advance. Kenneth from Ireland :)
Found 2 solutions by rapaljer, jsmallt9:
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi Kenneth,
You might want to visit my website and take a look at my FREE VIDEOS of me teaching LOGARITHMS in my own class a few years ago. It looks like you are SOLVING EXPONENTIAL EQUATIONS. For a complete explanation of LOGARITHMS, please see my own website. Click on my tutor name "Rapaljer" anywhere in algebra.com, and then click on my website that is given there. Look for the link "Basic, Intermediate, and College Algebra: One Step at a Time" and select "College Algebra", "Chapter 4". My explanations were written for students who have trouble understanding math, and according to my own students, much easier to understand than traditional textbooks.
I also have TWO complete videos from my classes before I retired in which I taught the lessons myself. The videos are FREE. Look for "Rapalje Videos in Living Color" on my Homepage.
Now, let me solve the problems that I have time for:

Since both base numbers are powers of 5, there is an easy way to do this:

When you raise a power to a power, you must MULIPLY the exponents:


Since the base numbers are equal, the exponents must be equal, so



In your second problem, in order to "undo" the e^, you should take the ln of each side of the equation:




Last problem, I'll help you set it up, but I don't have time to calculate it.

Start by taking the ln of each side:

By law of logarithms:

By distributive property:

Get all the x terms on one side by subtracting x* ln7 from each side. And get all the NON-x terms to the right side by subtracting 1*ln3 from each side:

Next, factor out the x on the left side, and divide by the resulting factor on the left side:

I think this is correct. I don't have time to check it, but I have a TON of these on my website on the page called "Solving Exponential Equations." Hang in there and good luck on your test!!
Dr. Robert J. Rapalje, Retired
Seminole State College of Florida
Altamonte Springs Campus
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Is this really the equation? Or is it:

or

The first equation is extremely difficult. The other two (which are equivalent to each other) are more like the problems given in Math classes. I am going to assume that the last one is correct.
Usually, when the variable is in an exponent, logarithms are used to solve the equation. The exception is when both sides of the equation can be expressed as powers of the same number.
Since  this equation is one of those that can be solved without logarithms. Substituting this equation is one of those that can be solved without logarithms. Substituting 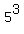 for 125 we get: for 125 we get:

The rule for exponents when raising a power to a power is to multiply the exponents. Using this rule (twice) to simplify the right side:


Both sides of the equation are now powers of 5. In order for these powers of 5 to be equal, the exponents must be equal. So:
x = 6x-6
This is an easy equation to solve. Subtracting 6x from each side:
-5x = -6
Dividing both sides by -5 we get:


In this equation we cannot express both sides as powers of the same number. So we will need to use logarithms. Logarithms of any base can be used. However, there are two things to consider when selecting a base:- Using a base for the logarithm that matches the base of one of the exponents will lead to a simpler expression for an answer.
- Using a base for the logarithm that your calculator "knows", like base 10 or base e (aka ln), will make it easier to find a decimal approximation of the answer.
So using base 3 or base 7 logarithms will make our answer simpler. But using base 10 or base e logarithms will make finding a decimal approximation easier. I am going to choose base 7:

Now we use a property of logarithms,  , to move the exponent of the argument out in front of the logarithm. It is this property which is the very reason we use logarithms on these equations. It allows us to move the exponent, where the variable is, to a place where we can use "regular" Algebra to solve it. Using this property on both sides we get: , to move the exponent of the argument out in front of the logarithm. It is this property which is the very reason we use logarithms on these equations. It allows us to move the exponent, where the variable is, to a place where we can use "regular" Algebra to solve it. Using this property on both sides we get:

By definition,  so this becomes: so this becomes:

On the left side we will use the Distributive Property to multiply:

Gathering the x terms on one side and the other terms on the other side (by subtracting x and 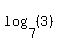 from each side) we get: from each side) we get:

Factoring out x we get:

And dividing both sides by 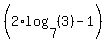 : :

This is an exact expression for the solution to the equation. If you want a decimal approximation it is not too late. We can use the base conversion formula,  , to convert the base 7 logarithms into either base 10 or base e logarithms. , to convert the base 7 logarithms into either base 10 or base e logarithms.
For the most part I will leave

for you to solve. One hint: There is a clear choice for the base of the logarithm to use. Base e logarithms will make the exact answer simpler (since it matches the base of the only exponential term) and it is a base your calculator "knows" so a decimal approximation of the answer will be easy.
|
|
|