SOLUTION: Hey, I'm trying to prove this sin(u+v)=sin(u)cos(v)+cos(u)sin(v) and I have no idea how. Thanks :)

Algebra ->  Trigonometry-basics -> SOLUTION: Hey, I'm trying to prove this sin(u+v)=sin(u)cos(v)+cos(u)sin(v) and I have no idea how. Thanks :)      Log On


   

Question 378302: Hey, I'm trying to prove this sin(u+v)=sin(u)cos(v)+cos(u)sin(v) and I have no idea how. Thanks :)
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!


By the law of sines,

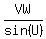
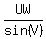
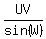VW%2Fsin%28U%29%22%22=%22%22UW%2Fsin%28V%29%22%22=%22%22UV%2Fsin%28W%29

Let those three fractions equal to a constant k,

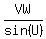
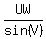
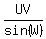
VW%2Fsin%28U%29%22%22=%22%22UW%2Fsin%28V%29%22%22=%22%22UV%2Fsin%28W%29%22%22=%22%22k

Then we have

VW = k*sin(U), UW = k*sin(V), UV = k*sin(W)

Draw altitude WX



VX = VW*cos(V) = k*sin(U)cos(V) 

UX = UW*cos(U) = k*sin(V)cos(U)

UV = VX + UX = k*sin(U)cos(V) + k*sin(V)cos(U)

UV = k*sin(W)

k*sin(W) = k*sin(U)cos(V) + k*sin(V)cos(U)

sin(W) = sin(U)cos(V) + sin(V)cos(U)

W = 180° - (U+V)

sin[180°-(U+V)] = sin(U)cos(V) + sin(V)cos(U)

and since the sine of the supplement of an angle 
equals the sine of the angle,

sin(U+V) = sin(U)cos(V) + sin(V)cos(U)

switch the factors in the last term

sin(U+V) = sin(U)cos(V) + cos(U)sin(V)

Edwin