3x - 6y + 1z = 0
1x + 1y + 0z = 0
-12x + 24y - 4z = 0
We make the augmented matrix by eliminating the variables:
Swap R1 and R2 (row 1 and row 2)
That instruction is written
R1<-->R2
Get a 0 where the 3 is by multiplying R1 by -3
temporarily and add it to row 2, then restore R1
That instruction is written
-3*R1+R2 -> R2
Get a 0 where the -12 is by multiplying R1 by 12
temporarily and add it to row 2, then restore R1
That instruction is written
12*R1+R3 --> R3
Get a 1 where the -9 is by multiplying row 2 by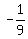 
That instruction is written:
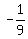R2 --> R2
Get a 0 where the 36 is by multiplying R2 by -36
temporarily and add it to row 3, then restore R2
That instruction is written
-36R2+R3-->R3
Write that as a system of equations:
or
We let z be arbitrary. Solve the second equation for y
Solve the first equation for x:
Substitute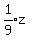 
for y
So the set of solutions is
(x,y,z) = (
,,
)
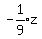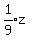where z is any arbitrary number.
Edwin
