 Get 0 on the right by subtracting 1 from both sides:
Get 0 on the right by subtracting 1 from both sides:
 Find the critical values of the left side by temporarily setting
it equal to 0. This temporary situation will be done only in green.
After finding the critical values we will return to the original
problem (in black).
Find the critical values of the left side by temporarily setting
it equal to 0. This temporary situation will be done only in green.
After finding the critical values we will return to the original
problem (in black).
 Add 1 to both sides:
Add 1 to both sides:
 Take logs base 2 of both sides:
Take logs base 2 of both sides:




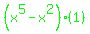





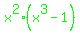

 Use the zero-factor principle by setting both factore = 0
Use the zero-factor principle by setting both factore = 0
 So the critical values are 0 and 1, so we can now
return to the black equation:
So the critical values are 0 and 1, so we can now
return to the black equation:
 We draw a number line and put open circles at the critical values.
The circles must be open because the cause the left side to become = 0,
not < 0.
-------------------o--------o------------------
-2 -1 0 1 2 3
We choose a value of x left of 0, say -1, and substitute it in
the equation:
We draw a number line and put open circles at the critical values.
The circles must be open because the cause the left side to become = 0,
not < 0.
-------------------o--------o------------------
-2 -1 0 1 2 3
We choose a value of x left of 0, say -1, and substitute it in
the equation:

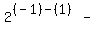



















 That is a true statement so we shade the part of
the number line left of 0
<==================o--------o------------------
-2 -1 0 1 2 3
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Next we choose a value of x between 0 and 1, say
That is a true statement so we shade the part of
the number line left of 0
<==================o--------o------------------
-2 -1 0 1 2 3
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Next we choose a value of x between 0 and 1, say 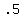 and substitute it in
the equation:
and substitute it in
the equation:

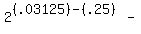



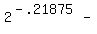










 That is also a true statement so we shade the part of
the number line between 0 and 1, not including either
one, of course
<==================o========o------------------
-2 -1 0 1 2 3
Next we choose a value of x right of 1, say 2, and substitute it in
the equation:
That is also a true statement so we shade the part of
the number line between 0 and 1, not including either
one, of course
<==================o========o------------------
-2 -1 0 1 2 3
Next we choose a value of x right of 1, say 2, and substitute it in
the equation:





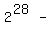



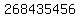






 That is a false statement so we do not shade the part of
the number line right of 1, so the solution is indicated by
the number line:
<==================o========o------------------
-2 -1 0 1 2 3
The interval notation for that is:
That is a false statement so we do not shade the part of
the number line right of 1, so the solution is indicated by
the number line:
<==================o========o------------------
-2 -1 0 1 2 3
The interval notation for that is:






 Edwin
Edwin