SOLUTION: * The probability of a successful assembly of a product in a manufacturing process is 0.8. i) What is the probability that the first successful assembly requires exactly four tr

Algebra ->  Probability-and-statistics -> SOLUTION: * The probability of a successful assembly of a product in a manufacturing process is 0.8. i) What is the probability that the first successful assembly requires exactly four tr      Log On


   

Question 376519: * The probability of a successful assembly of a product in a manufacturing process is 0.8.
i) What is the probability that the first successful assembly requires exactly four trials?
ii) What is the probability that the first successful assembly requires at least four trials?
iii) What is the probability that the first successful assembly requires at most four trials?iv) What assumptions did you make, if any, to solve this problem?

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
* The probability of a successful assembly of a product in a manufacturing process is 0.8.
i) What is the probability that the first successful assembly requires exactly four trials?
Probability of a success is 0.8 
Probability of a failure is 1 - 0.8 = 0.2

P(failure 1st AND failure 2nd AND failure 3rd AND success 4th) =

P(failure 1st)*P(failure 2nd)*P(failure 3rd)*P(success 4th) =


%280.2%29%280.2%29%280.2%29%280.8%29+=++%28.02%29%5E3%280.8%29+=+0.0064

ii) What is the probability that the first successful assembly requires at least four trials?
The probability that the first successful attempt will be the nth trial is

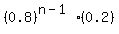%280.8%29%5E%28n-1%29%2A%280.2%29

That is the nth term of an infinite geometric series with first term
a%5B1%5D=0.0064 and common ratio r = 0.8.

That sum is given by

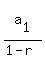
S%5Binfinity%5D%22%22=%22%22a%5B1%5D%2F%281-r%29

S%5Binfinity%5D%22%22=%22%220.0064%2F%281-0.8%29=0.0064%2F0.2=0.032

iii) What is the probability that the first successful assembly requires at most four trials?
The probability that the first successful attempt will be the nth trial is

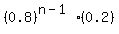%280.8%29%5E%28n-1%29%2A%280.2%29

So

The probability that the first successful attempt will be the 1st trial is

%280.8%29%5E%281-1%29%2A%280.2%29=%280.8%29%5E0%2A%280.2%29=1%2A0.2=0.2

The probability that the first successful attempt will be the 2nd trial is

%280.8%29%5E%282-1%29%2A%280.2%29=%280.8%29%5E1%2A%280.2%29=%280.8%29%280.2%29=0.16

The probability that the first successful attempt will be the 3rd trial is

%280.8%29%5E%283-1%29%2A%280.2%29=%280.8%29%5E2%2A%280.2%29=%280.64%29%280.2%29=0.128

The probability that the first successful attempt will be the 4th trial is

%280.8%29%5E%284-1%29%2A%280.2%29=%280.8%29%5E3%2A%280.2%29=%280.512%29%280.2%29=0.1024

The required probability is the sum of those

0.2 + 0.16 + 0.128 + 0.1024 = 0.5904

iv) What assumptions did you make, if any, to solve this problem?
The assumption that the trials are independent, that is, the assumption
that previous successful or failing trials do not affect the probability 
of present or future trials being successful or failing.

Edwin