SOLUTION: 3log(2x-1)=1

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: 3log(2x-1)=1       Log On


   

Question 374794: 3log(2x-1)=1
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
3log(2x-1) = 1
To solve a logarithmic equation like this, where the variable is in the argument (or base) of a logarithm, you often start by transforming the equation into one of the following forms:
log(expression) = other-expression
or
log(expression) = log(other-expression)

Your equation is very close to the first form. The 3 in front is not part of the form so we need to get rid of it. There are two ways we can eliminate the 3:
  1. Divide both sides of the equation by 3. This gives us
    log%28%282x-1%29%29+=+1%2F3
  2. Using a property of logarithms, q%2Alog%28a%2C+%28p%29%29+=+log%28a%2C+%28p%5Eq%29%29, to "move" the coefficient into the argument as an exponent. This gives us:
    log%28%28%282x-1%29%5E3%29%29+=+1

Either way we end up with the first form. The next step is to rewrite the equation in exponential form. In general, log%28a%2C+%28p%29%29+=+q is equivalent to p+=+a%5Eq.
Depending on how you eliminated the 3 you have either
log%28%282x-1%29%29+=+1%2F3
or
log%28%28%282x-1%29%5E3%29%29+=+1
I will solve both.
Solving log%28%282x-1%29%29+=+1%2F3
Rewrite in exponential form:
2x-1+=+10%5E%281%2F3%29
Since an exponent of 1/3 means cube root, this can be written as:
2x-1+=+root%283%2C+10%29
Adding 1 to each side we get:
2x+=+1+%2B+root%283%2C+10%29
Dividing by 2 we get:
x+=+%281+%2B+root%283%2C+10%29%29%2F2

Solving log%28%28%282x-1%29%5E3%29%29+=+1
Rewrite in exponential form:
%282x-1%29%5E3+=+10%5E1
which simplifies to:
%282x-1%29%5E3+=+10
Find the cube root of each side:
root%283%2C+%282x-1%29%5E3%29+=+root%283%2C+10%29
which simplifies to:
2x-1+=+root%283%2C+10%29
(Note that we reached the same equation when solving log%28%282x-1%29%29+=+1%2F3. So we will end up with the same answer this way.)
Adding 1 to each side we get:
2x+=+1+%2B+root%283%2C+10%29
Dividing by 2 we get:
x+=+%281+%2B+root%283%2C+10%29%29%2F2

When solving logarithmic equations, it is important to check your answers. You must ensure that all arguments (and bases) of logarithms are positive! And when checking your answers, use the original equation:
3log(2x-1) = 1
Checking x+=+%281+%2B+root%283%2C+10%29%29%2F2:
3log%28%282%28%281+%2B+root%283%2C+10%29%29%2F2%29-1%29%29+=+1
The 2's cancel in the argument:
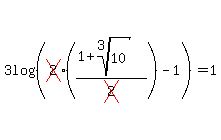
3log%28%28cross%282%29%28%281+%2B+root%283%2C+10%29%29%2Fcross%282%29%29-1%29%29+=+1
leaving
3log%28%28%281+%2B+root%283%2C+10%29%29-1%29%29+=+1
The 1 and -1 cancel out (since they add up to zero):
3log%28%28root%283%2C+10%29%29%29+=+1
At this point we can see that the argument to the logarithm is positive. Finishing the check will determine if we made a mistake. I can see that our answer is correct. If you can't see this, then finish the check.

NOTE: If you find that an answer makes an argument (or base) of a logarithm zero or negative (i.e. not positive)...
  • It does not mean you made a mistake while solving the equation! This is just something that could happen any time you solve a logarithmic equation. This is why is it important to check for this!
  • You reject that answer, even if it is the only answer you found! If you have to reject your only answer, then it means that there are no solutions to the equation.