SOLUTION: An ordinary (fair) die is a cube with the numbers 1 through 6 on the sides (represented by painted spots). Imagine that such die is rolled twice in succession and that the face val

Algebra ->  Probability-and-statistics -> SOLUTION: An ordinary (fair) die is a cube with the numbers 1 through 6 on the sides (represented by painted spots). Imagine that such die is rolled twice in succession and that the face val      Log On


   

Question 373964: An ordinary (fair) die is a cube with the numbers 1 through 6 on the sides (represented by painted spots). Imagine that such die is rolled twice in succession and that the face values of the two rolls are added together. This sum is recorded as the outcome of a single trail of a random experiment.
Compute the probability of each of the following events:
Event A: the sum is greater than 5.
Event B: the sum is divisible by 5.
Write your answers as exact fractions.
P(A)=
P(B)=
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!

Here are all the 36 ways the two rolls could come up,
and they are all equally likely.

(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)
 
(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)
 
(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)
 
(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)
 
(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)
 
(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)

Event A: the sum is greater than 5.
I will color the ones red which have a sum greater than 5:


(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)
 
(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)
 
(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)
 
(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)
 
(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)
 
(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)

There are 26 out of the entire 36 that have a sum greater than 5, so

P(A) = 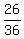26%2F36 which reduces to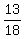 13%2F18

Event B: the sum is divisible by 5.
I will color the ones green which have a sum divisible by 5. The
only sums divisible by 5 are sums 5 and 10:

(1,1)  (1,2)   (1,3)  (1,4)   (1,5)  (1,6)
 
(2,1)  (2,2)   (2,3)  (2,4)   (2,5)  (2,6)
 
(3,1)  (3,2)   (3,3)  (3,4)   (3,5)  (3,6)
 
(4,1)  (4,2)   (4,3)  (4,4)   (4,5)  (4,6)
 
(5,1)  (5,2)   (5,3)  (5,4)   (5,5)  (5,6)
 
(6,1)  (6,2)   (6,3)  (6,4)   (6,5)  (6,6)

There are 7 out of the entire 36 that have a sum divisible by 5, so

P(B) = 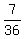7%2F36 



Edwin