SOLUTION: 1/2 log base a of (x+2) + 1/2 log base a of (x-2) = 2/3 log base a of 27

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: 1/2 log base a of (x+2) + 1/2 log base a of (x-2) = 2/3 log base a of 27      Log On


   

Question 373280: 1/2 log base a of (x+2) + 1/2 log base a of (x-2) = 2/3 log base a of 27
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!

With equations with the variable in one or more arguments (or bases) of logarithms, you often start by transforming the equation into one of the following forms:
log(expression) = other-expression
or
log(expression) = log(other-expression)

Since your equation has no "non-log" terms, we will aim for the second form. The coefficients of the logarithms in the second form are 1's. Your equation's logarithms have other coefficients. Fortunately we have a property of logarithms, q%2Alog%28w%2C+%28p%29%29+=+log%28w%2C+%28p%5Eq%29%29 which allows us to "move" a coefficient of a logarithm into the argument as an exponent. Using this on your three logarithms we get:

An exponent of 1/2 means square root. So I am going to replace the arguments which have this exponent with square roots:

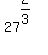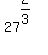
Also, 27%5E%282%2F3%29 will simplify
27%5E%282%2F3%29
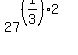
27%5E%28%281%2F3%29%2A2%29
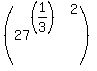
%2827%5E%28%281%2F3%29%29%5E2%29
%28root%283%2C+27%29%5E2%29
Since 3%5E3+=+27, root%283%2C+27%29+=+3:
3%5E2
9
So 27%5E%282%2F3%29+=+9. This makes our equation:

The coefficients are now the 1's we wanted. Next we need to combine the two logarithms into one. And we have a property of logarithms, log%28w%2C+%28p%29%29+%2B+log%28w%2C+%28q%29%29+=+log%28w%2C+%28p%2Aq%29%29, which allows us to do just that! Using this property on the left side we get:
log%28a%2C+%28sqrt%28x%2B2%29%2Asqrt%28x-2%29%29%29+=+log%28a%2C+%289%29%29
which, using a property of radicals, root%28w%2C+p%29%2Aroot%28w%2C+q%29+=+root%28w%2C+p%2Aq%29, simplifies to:
log%28a%2C+%28sqrt%28%28x%2B2%29%2A%28x-2%29%29%29%29+=+log%28a%2C+%289%29%29
We finally have achieved the second form! From here we use some basic logic:
If the base a logarithms of two expressions are equal then the two expressions must be equal. So:
sqrt%28%28x%2B2%29%2A%28x-2%29%29+=+9
To solve this we need to eliminate the square root. So we square both sides:
%28sqrt%28%28x%2B2%29%2A%28x-2%29%29%29%5E2+=+%289%29%5E2
which simplifies as follows:
%28x%2B2%29%2A%28x-2%29+=+81
x%5E2+-+4+=+81
Adding 4 to each side we get:
x%5E2+=+85
Finding the square root of each side:
sqrt%28x%5E2%29+=+sqrt%2885%29
abs%28x%29+=+sqrt%2885%29
x+=+sqrt%2885%29 or x+=+-sqrt%2885%29

Whenever you are solving a logarithmic equation you must check your answers (at least to make sure all arguments and bases of logarithms are not zero or negative). And whenever you square both sides of an equation you must check for extraneous solutions. (Extraneous solutions are solutions which work in the squared equation but do not work in the original equation. We have a logarithmic equation and we squared both sides!

When checking, use the original equation:

Checking x+=+sqrt%2885%29:

Using our properties again:




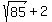Using the %28p%2Bq%29%28p-q%29+=+p%5E2+-+q%5E2 to multiply sqrt%2885%29%2B2%29%2Asqrt%2885%29-2%29 we get:
log%28a%2C+%28sqrt%28%28sqrt%2885%29%29%5E2+-+2%5E2%29%29%29+=+log%28a%2C+%289%29%29
log%28a%2C+%28sqrt%2885+-+4%29%29%29+=+log%28a%2C+%289%29%29
log%28a%2C+%28sqrt%2881%29%29%29+=+log%28a%2C+%289%29%29
log%28a%2C+%289%29%29+=+log%28a%2C+%289%29%29 Check!!

Checking x+=+-sqrt%2885%29:

Already we can see that the two arguments on the left side will be negative (since 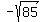-sqrt%2885%29 is -9.something). Since arguments of logarithms can never be negative, we must reject this solution!

So the only solution to your equation is x+=+sqrt%2885%29