SOLUTION: (e^x - e^-x)/2 =-2

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: (e^x - e^-x)/2 =-2      Log On


   

Question 372994: (e^x - e^-x)/2 =-2
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
%28e%5Ex+-+e%5E%28-x%29%29%2F2+=-2
One way to solve this is based on recognizing that the left side is sinh(x) which makes your equation:
sinh(x) = -2
(If you have never heard of sinh (hyperbolic sine), then skip down to "Without sinh" below.)
To find x, then we just have to solve
sinh-1(-2) = x
You may have a button for sinh-1 on your calculator. Or you may know the formula:
sinh-1(x) = ln(x + sqrt%28x%5E2+%2B+1%29)
which makes
sinh-1(-2) = ln((-2) + sqrt%28%28-2%29%5E2+%2B+1%29)
which simplifies to:
sinh-1(-2) = ln(-2 + 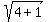sqrt%284+%2B+1%29)
sinh-1(-2) = ln(-2 + sqrt%285%29)
which is an exact expression for your answer.


%28e%5Ex+-+e%5E%28-x%29%29%2F2+=-2
Solving this without recognizing hyperbolic sine or without know how to work with hyperbolic functions, we start by multiplying both sides by 2 (to get rid of the fraction:
e%5Ex+-+e%5E%28-x%29+=-4
Next we can rewrite the 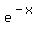e%5E%28-x%29 with a positive exponent:
e%5Ex+-+1%2Fe%5Ex+=-4
By doing this now have another fraction. This gives us a clue about what to do next. We want to eliminate the fraction so we will multiply by e%5Ex:
e%5Ex%28e%5Ex+-+1%2Fe%5Ex%29+=+e%5Ex%28-4%29
On the left side we need to use the Distributive Property:
e%5Ex%2Ae%5Ex+-+e%2Ax%2A%281%2Fe%5Ex%29+=+e%5Ex%28-4%29
which simplifies to:
e%5E%282x%29+-+1+=+-4e%5Ex
Next we add 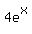4e%5Ex to each side:
e%5E%282x%29+%2B4e%5Ex+-+1+=+0
Since the exponent of e in the first term is twice the exponent of e in the second term, this equation is in quadratic form for e%5Ex. This means we can use methods for solving quadratic equations on this equation. (If you have trouble seeing this, see "Using a temporary variable" below.) This equation won't factor but we can use the Quadratic Formula:
e%5Ex+=+%28-%284%29+%2B-+sqrt%28%284%29%5E2+-+4%281%29%28-1%29%29%29%2F2%281%29
which simplifies as follows:
e%5Ex+=+%28-%284%29+%2B-+sqrt%2816+-+4%281%29%28-1%29%29%29%2F2%281%29
e%5Ex+=+%28-%284%29+%2B-+sqrt%2816+%2B+4%29%29%2F2%281%29
e%5Ex+=+%28-%284%29+%2B-+sqrt%2820%29%29%2F2%281%29
e%5Ex+=+%28-4+%2B-+sqrt%2820%29%29%2F2
e%5Ex+=+%28-4+%2B-+sqrt%284%2A5%29%29%2F2
e%5Ex+=+%28-4+%2B-+sqrt%284%29%2Asqrt%285%29%29%2F2
e%5Ex+=+%28-4+%2B-+2%2Asqrt%285%29%29%2F2
e%5Ex+=+%282%28-2+%2B-+sqrt%285%29%29%29%2F2
e%5Ex+=+%28cross%282%29%28-2+%2B-+sqrt%285%29%29%29%2Fcross%282%29
e%5Ex+=+-2+%2B-+sqrt%285%29
In long form this is:
e%5Ex+=+-2+%2B+sqrt%285%29 or e%5Ex+=+-2+-+sqrt%285%29
The right side of the second equation is clearly negative. But powers of e cannot be negative. So there are no solutions to the second equation. The right side of the first equation, because sqrt%285%29+%3E+2, is a positive number. So we will get a solution from it. We just find the base e logarithm (ln) of each side:
ln%28e%5Ex%29+=+ln%28-2+%2B+sqrt%285%29%29
On the left side we use the property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponent of the argument out in front:
x%2Aln%28e%29+=+ln%28-2+%2B+sqrt%285%29%29
By definition ln(e) = 1 so this simplifies to:
x+=+ln%28-2+%2B+sqrt%285%29%29
which is the same answer as we got with the hyperbolic sine.

Using a temporary variable
Until you have had some practice, equations in quadratic form can be hard to solve the I did above. A temporary variable can help make what I did easier to understand. With the equation:
e%5E%282x%29+%2B4e%5Ex+-+1+=+0
we still have to recognize that the first exponent is twice the second exponent. But instead of going straight to solving it we can use a temporary variable:
Let q = e%5Ex
Then q%5E2+=+%28e%5Ex%29%5E2+=+e%5E2x
Substituting these into our equation we get:
q%5E2+%2B4q+-+1+=+0
This is obviously a quadratic equation. Using the Quadratic formula on this we get:
q+=+%28-%284%29+%2B-+sqrt%28%284%29%5E2+-+4%281%29%28-1%29%29%29%2F2%281%29
which simplifies as follows:
q+=+%28-%284%29+%2B-+sqrt%2816+-+4%281%29%28-1%29%29%29%2F2%281%29
q+=+%28-%284%29+%2B-+sqrt%2816+%2B+4%29%29%2F2%281%29
q+=+%28-%284%29+%2B-+sqrt%2820%29%29%2F2%281%29
q+=+%28-4+%2B-+sqrt%2820%29%29%2F2
q+=+%28-4+%2B-+sqrt%284%2A5%29%29%2F2
q+=+%28-4+%2B-+sqrt%284%29%2Asqrt%285%29%29%2F2
q+=+%28-4+%2B-+2%2Asqrt%285%29%29%2F2
q+=+%282%28-2+%2B-+sqrt%285%29%29%29%2F2
q+=+%28cross%282%29%28-2+%2B-+sqrt%285%29%29%29%2Fcross%282%29
q+=+-2+%2B-+sqrt%285%29
In long form this is:
q+=+-2+%2B+sqrt%285%29 or q+=+-2+-+sqrt%285%29
Next we substitute back in for q:
e%5Ex+=+-2+%2B+sqrt%285%29 or e%5Ex+=+-2+-+sqrt%285%29
The right side of the second equation is clearly negative. But powers of e cannot be negative. So there are no solutions to the second equation. The right side of the first equation, because sqrt%285%29+%3E+2, is a positive number. So we will get a solution from it. We just find the base e logarithm (ln) of each side:
ln%28e%5Ex%29+=+ln%28-2+%2B+sqrt%285%29%29
On the left side we use the property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponent of the argument out in front:
x%2Aln%28e%29+=+ln%28-2+%2B+sqrt%285%29%29
By definition ln(e) = 1 so this simplifies to:
x+=+ln%28-2+%2B+sqrt%285%29%29
which is the same answer as we got with both of the solutions above.