Question 372207: 12e^2x=5^x I need to solve for x and i dont know how too
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
With equations where the variable is in one or more exponents, like yours, we often use logarithms to solve. So first we find the logarithm of each side. The base of logarithm does not matter in any significant way. But in this equation, since the base on the left side is e and since many calculators "know" base e logarithms (aka ln), I am going to choose base e logarithms:
Next we use a property of logarithms,  , to split the first logarithm (separating the 12 from the  ):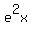
Next we can use another property of logarithms,  , to "move" the exponents of the arguments out in front. (This property of logarithms is the very reason we use logarithms. It allows us to move the variable out the exponents. And we had to split the 12 away first because the exponent of 2x only applied to the e, not the 12.):
ln(12) + (2x)ln(e) = x*ln(5)
Since ln(e) = 1 by definition this simplifies to:
ln(12) + 2x = x*ln(5)
Now we can solve for x. We start by gathering the x terms on one side of the equation. I'll subtract 2x from each side:
ln(12) = x*ln(5) - 2x
Then we factor out x on the right side:
ln(12) = x*(ln(5) - 2)
And last of all, divide both sides by: (ln(5) - 2):
This is an exact expression for the solution to your equation. If you want a decimal approximation, then get out your calculator, find the two logarithms and simplify the expression.
|
|
|
