SOLUTION: Please Factor: 24j^2 - 14j - 3

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Please Factor: 24j^2 - 14j - 3      Log On


   

Question 372004: Please Factor:
24j^2 - 14j - 3
Found 2 solutions by Fombitz, jsmallt9:
Answer by Fombitz(32388) About Me  (Show Source):
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!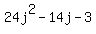
24j%5E2+-+14j+-+3
This is a trinomial which does not fit any of the factoring patterns. This means we will have to try various combinations of the factors of 24, the leading coefficient, and 3, the constant term. Since 24 has quite a few pairs of factors this could take some time.

When it look like a trinomial might take a lot of trial and error, you might want to consider the following:
  • Pretend the expression is equal to zero:
    24j%5E2+-+14j+-+3+=+0
  • Use the Quadratic Formula:
    j+=+%28-%28-14%29+%2B-+sqrt%28%28-14%29%5E2-4%2824%29%28-3%29%29%29%2F%282%2824%29%29
    j+=+%28-%28-14%29+%2B-+sqrt%28196-4%2824%29%28-3%29%29%29%2F%282%2824%29%29
    j+=+%28-%28-14%29+%2B-+sqrt%28196%2B288%29%29%2F%282%2824%29%29
    j+=+%28-%28-14%29+%2B-+sqrt%28484%29%29%2F%282%2824%29%29
    Since the radicand has turned out to be a perfect square (484 = 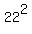22%5E2) we know that the expression will factor. If the radicand had not been a perfect square then the expression will not factor (at least not in any usual way).
    j+=+%28-%28-14%29+%2B-+22%29%2F%282%2824%29%29
    j+=+%2814+%2B-+22%29%2F48
    j+=+36%2F48 or j+=+%28-8%29%2F48
    j+=+3%2F4 or j+=+%28-1%29%2F6
  • These "solutions" to the equation we made up tell us what the factors are. If the solutions had been whole numbers the factors would be in the form: (j - solution). Since they are fractions the factors are in form: (d*j - n) where d = the denominator and n equals the numerator of the "solution". So the factors for 3/4 and -1/6 are:
    (4j-3) and (6j - (-1))
    or
    (4j-3) and (6j + 1)

So
24j%5E2+-+14j+-+3+=+%284j-3%29%286j%2B1%29
which is the same answer we would get if we had taken the time to find the one and only combination of factors of 24 and 3.

P.S. In response to your question in your "Thank you"...
You are correct in thinking that patterns will not work on your expression. But patterns are not the only way to factor your expression.

As I tried to explain above, using the Quadratic Formula is an alternative way to factor. (It isn't often taught but I thought you might like to see it.) If you haven't learned the Quadratic Formula then clearly should should not try to use it in this way.

Instead there is yet another way, as I mentioned above, to factor your expression. And that is to find the right combination of factors of 24 and 3. You just try different combinations, in a trial and error way, until you find the one combination which, when multiplied together, actually works out to be 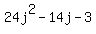24j%5E2+-+14j+-+3. For example:
(24j + 1)(j - 3) which works out to be 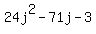24j%5E2+-+71j+-+3
(24j - 1)(j + 3) which works out to be 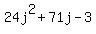24j%5E2+%2B+71j+-+3
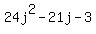
(24j + 3)(j - 1) which works out to be 24j%5E2+-+21j+-+3
(24j - 3)(j + 1) which works out to be 24j%5E2+%2B+21j+-+3
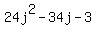
(12j + 1)(2j - 3) which works out to be 24j%5E2+-+34j+-+3
(12j - 1)(2j + 3) which works out to be 24j%5E2+%2B+34j+-+3
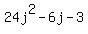
(12j + 3)(2j - 1) which works out to be 24j%5E2+-+6j+-+3
(12j - 3)(2j + 1) which works out to be 24j%5E2+%2B+6j+-+3
None of these work out to be 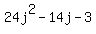24j%5E2+-+14j+-+3. If you methodically go through all the different combinations, you will, sooner or later, end up trying:
(4j-3)(6j+1) which works out to be 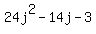24j%5E2+-+14j+-+3
This is the only combination that will work!

As you can see, this trial and error technique for factoring trinomials, especially when there a lot of possible combinations, can take a long time. That is why I showed you the Quadratic Formula. The formula is not the easiest to work with but some like using it in a situation like this because it is a fairly direct way to find out
  • If it factors at all
  • the right combination of factors (if the expression does factor).