SOLUTION: I do not know what formula to use to solve problems of this nature. Here is the problem: If Steven can mix 20 drinks in 5 minutes, Sue can mix 20 drinks in 10 minutes, and Jack

Algebra ->  Rate-of-work-word-problems -> SOLUTION: I do not know what formula to use to solve problems of this nature. Here is the problem: If Steven can mix 20 drinks in 5 minutes, Sue can mix 20 drinks in 10 minutes, and Jack       Log On


   

Question 37132: I do not know what formula to use to solve problems of this nature.
Here is the problem: If Steven can mix 20 drinks in 5 minutes, Sue can mix 20 drinks in 10 minutes, and Jack can mix 20 drinks in 15 minutes, how much time will it take all 3 of them working together to mix the 20 drinks?
Can you help
Found 5 solutions by josmiceli, amalm06, ikleyn, MathTherapy, greenestamps:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
There are 3 "rates" of mising drinks
Steven's rate = 20 drinks / 5 min.
Sue's rate = 10 drinks / 10 min.
Jack's rate = 20 drinks / 15 min.
The formula I use is
number of drinks / their combined rates = time
20 / (20/5 + 20/10 + 20/15) = t
factor out 20 in the denominator
20 / 20(1/5 + 1/10 + 1/15) = t
the 20's cancel
1 / (1/5 + 1/10 + 1/15) = t
common denominator is 30
1 / (6/30 + 3/30 + 2/30) = t
1 / (11/30) = t
30/11 = t
t = 2.73 min.

Answer by amalm06(224) About Me  (Show Source):
You can put this solution on YOUR website!
Steven: dW1/dt=4 --> dW1= 4 dt
Sue: dW2/dt=2 --> dW2= 2 dt
Jack: dW3/dt=1.333 --> dW3 = 1.333 dt

W=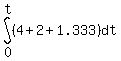int%28+%284%2B2%2B1.333%29%2C+dt%2C+0%2C+t+%29=1

7.333t = 1

t=0.136 (total time for 1 drink)

The time taken to make twenty drinks is 0.136*20=2.73 min (Answer)

Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!
.
Steven's rate of work is  20%2F5  = 4 drinks per minute.


Sue's    rate of work is  20%2F10 = 2 drinks per minute.


Jack's   rate of work is  20%2F15 = 4%2F3 drinks per minute.


Their combined rate of work is  4 + 2 + 4%2F3 = 12%2F3+%2B+6%2F3+%2B+4%2F3 = 22%2F3  drinks per minute.


It means that 3 of them, working together, will mix 20 drinks in   20%2F%28%2822%2F3%29%29 = %2820%2A3%29%2F22 = 60%2F22 = 30%2F11 minutes = 28%2F11 minutes =  

    = 2 minutes and 43.64 seconds (approximately).

Solved.

----------------
It is a typical joint work problem.

To see many other similar solved joint work problems, look into the lessons
    - Using Fractions to solve word problems on joint work
    - Solving more complicated word problems on joint work
    - Selected joint-work word problems from the archive


Read them and get be trained in solving joint-work problems.

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems"  of the section  "Word problems".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.


Answer by MathTherapy(10549) About Me  (Show Source):
You can put this solution on YOUR website!
I do not know what formula to use to solve problems of this nature.
Here is the problem: If Steven can mix 20 drinks in 5 minutes, Sue can mix 20 drinks in 10 minutes, and Jack can mix 20 drinks in 15 minutes, how much time will it take all 3 of them working together to mix the 20 drinks?
Can you help
Steven can do the job (mix 20 drinks) in 5 minutes, or 1%2F5 of job in 1 minute

Sue can do the job (mix 20 drinks) in 10 minutes, or 1%2F10 of job in 1 minute

Jack can do the job (mix 20 drinks) in 15 minutes, or 1%2F15 of job in 1 minute

With T being time it takes all 3 to do the job (mix 20 drinks), we then get:  

%281%2F5%29+%2A+T+%2B+%281%2F10%29+%2A+T+%2B+%281%2F15%29+%2A+T+=+1

T%2F5+%2B+T%2F10+%2B+T%2F15+=+1

6T + 3T + 2T = 30 --------- Multiplying by LCD, 30

11T = 30

T, or time taken by the three working together, to do the job = 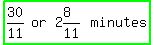highlight_green%28matrix%281%2C4%2C+30%2F11%2C+or%2C+2%268%2F11%2C+minutes%29%29

Answer by greenestamps(13195) About Me  (Show Source):
You can put this solution on YOUR website!


You have three responses so far to your question, all with different methods for solving the problem. Here is another method that many students find easier....

Find the least common multiple of the numbers of minutes each worker takes to mix the 20 drinks; then find the number of drinks the three of them could mix in that amount of time; then find how long it would take them together to make the 20 drinks.

The times for the three workers are 5, 10, and 15 minutes; the least common multiple is 30 minutes.
In 30 minutes, Steven could mix 120 drinks, Sue could mix 60, and Jack could mix 40.
Together in 30 minutes the three of them could mix 120+60+40=220 drinks.
So the time it would take the three of them to mix 20 = 220/11 drinks is 30/11 minutes.