Question 37102: I could really use some help on this.
An open-top box is to be constructed from a 4 by 6 foot rectangular cardboard by cutting out equal squares at each corner and then folding up the flaps. let x denote the length of each side of the square to be cut out.
A. Find the function V that represents the colume of the box in terms of x.
B. Graph the function and show the graph over the valid range of the variable x.
C. Using the graph, what is the value of x that will produce the maximum volume?
Answer by longjonsilver(2297)   (Show Source):
You can put this solution on YOUR website! ok... draw a 4x6 rectangle. Draw a little dotted square in each corner, of length x.
Once these are gone, the flaps will be folded up to form a box, whose base is now (4-2x) by (6-2x). And the height of the box is x.
Right then, the volume, V is now given by:
 , which when expanded is 
b. You should know what a cubic looks like. From this initial knowledge, we know its roots are satisfied by  . This means that either x=0 or 4-2x=0 or 6-2x=0. Hence, roots are at x=0, x=2, x=3.
A suitable range of values would be from x=0 (where the box actually has no height ie no volume) upto say x=2. This upper limit would be nonesensical since removing a square of size x=2 would mean cutting a whole side off the rectangle (since its width is only 4 to begin with... remember 2 squares are removed from each side).
So, plot:
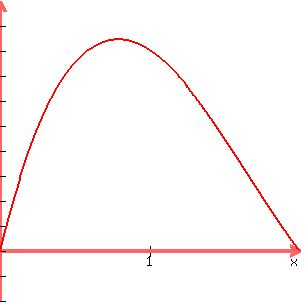
As for the maximum, you can find this algebraically if you know how. It looks like you don't since it says look on the graph.
You are expecting a maximum value at just before x=0.8. The exact answer is 
jon.
|
|
|
