Question 370575: Liz commutes 30 mi. to her job each day. She Finds that if she drives 10 mi/h faster it takes her 6 minutes less to get to work. Find her new speed.
I tried setting this problem up on a chart. For some reason when I worked the problem out I came out with really odd fractions, and I am not quite sure what I have done wrong. Any kind of help would truly mean a lot to me.
Found 2 solutions by ewatrrr, jim_thompson5910:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
Let r represent her old speed
d = r*t
30 = r*t
30/r = t


Multiplying thru by 10r(r+10) so as all denominators = 1
300r = 300(r+10) - r(r+10)
300r = 300r + 3000 - r^ - 10r
r^2 + 10r - 3000 = 0
factor
(x + 60)(x-50) = 0
x + 60)= 0 x = -60 cannot use
(x-50) = 0 x = 50mph her old speed. Her new speed would be 60mph( 10mph faster)
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let r = original speed.
and let t = time to get to work driving that original speed.
So if "Liz commutes 30 mi. to her job each day", this means that  because we're using the formula because we're using the formula  where the distance is where the distance is 
So the first equation is 
In addition, because "she drives 10 mi/h faster it takes her 6 minutes less to get to work", we can say that 
Notes: since she drives 10 mph faster, her new speed is r+10. Also, because 60 min = 1 hour, this means that 6 min =  hours. So if it takes 6 mins or hours. So if it takes 6 mins or  or an hour less, then the new time is or an hour less, then the new time is 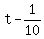
So the second equation is 
-----------------------------------------------------------
Now let's use both equations to solve for t and r
 Start with the first equation. Start with the first equation.
 Divide both sides by t to isolate r. Divide both sides by t to isolate r.
 Flip the equation. Flip the equation.
 Move onto the second equation. Move onto the second equation.
 Plug in Plug in 
 Multiply 10 by Multiply 10 by 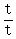
 Combine the fractions. Combine the fractions.
 Distribute Distribute
 Multiply. Multiply.
Note: the 't' terms cancel in the first fraction while in the second, we're dividing each term by 10.
 Multiply EVERY term by the LCD 't' to clear out the fractions. Multiply EVERY term by the LCD 't' to clear out the fractions.
 Distribute. Distribute.
 Subtract 30t from both sides. Subtract 30t from both sides.
 Combine like terms. Combine like terms.
Notice that the quadratic  is in the form of is in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for "t":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate  to get to get  . .
 Square Square  to get to get  . .
 Multiply Multiply 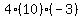 to get to get 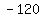
 Rewrite Rewrite 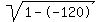 as as 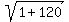
 Add Add  to to  to get to get 
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of  to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the possible solutions are  or or 
However, since a negative time isn't possible, this means that the only solution for 't' is 
Remember that 't' is the time in hours. So convert to minutes to get  minutes minutes
So the time it takes to travel 30 miles at the original speed is 36 minutes.
Recall that we made  . So plug . So plug  into the equation to get into the equation to get 
So her original speed is 50 mph. Add 10 mph to this speed to get 50+10 = 60 mph
So her new speed is 60 mph.
I'll leave the check to you. Remember to use the formula 
If you need more help, email me at jim_thompson5910@hotmail.com
Also, feel free to check out my tutoring website
Jim
|
|
|