Question 370456: Find the exact length of the altitude of an equilateral triangle each of whose sides measures 14.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! It may help to draw a picture. Draw an equilateral triangle. Since all the sides are congruent, all the angles are congruent, too. Since the angles of a triangle add up to 180 degrees and since all 3 angles for this triangle are the same, each angle must be 60 degrees.
Now draw in an altitude. (An altitude is a segment from a vertex to the opposite side, forming a right angle with the opposite side.
From here there are two paths we can follow. One uses the Pythagorean Theorem and the other uses the relationships between the sides of 30/60/90 right triangles. I will do both.
Pythagorean Theorem:
If the drawing is reasonably accurate, the altitude should should appear to split the original triangle exactly in two. It should look this way because the altitude does split the equilateral triangle into two congruent right triangles. We know this because we know two of the angles in each right triangle. They are 90 and 60. This means the third angles are both 30. And since the altitude is a side shared between the two triangles. So by ASA the two right triangles are congruent. And if they are congruent their corresponding parts are congruent. This means that the altitude, where it intersects the opposite side must bisect the opposite side. Since the entire opposite side is 14 then the two halves are 7.
Now we have the hypotenuse, 14, and one of the legs, 7, of a right triangle. With the Pythagorean Theorem:
 where x is the length of the second leg (which is the altitude).
Simplifying this we get:
Solving for x we start by subtracting 49:
Then we find the square root of each side. (We will discard the negative square root since sides of triangles cannot be negative.)
At last we simplify the square root. This is done by finding perfect square factors, if any:
Then, using a basic property of radicals,  , we can rewrite it with the perfect square in its own square root:
Since  :
which is the exact length of the altitude.
Using the relationships between the sides of 30/60/90 right triangles.
The rations between two sides of 30/60/90 triangles are always the same:- The ratio of the hypotenuse to the side opposite the 30 degree angle is always 2 no matter how big or small the triangle!
- The ratio of the side opposite to the 60 degree angle to the side opposite the 30 degree angle is always
 .
Using the first ratio:
hypotenuse/(opp. 30) = 2
Our hypotenuse is 14 so
14/(opp. 30) = 2
This makes the side opposite 30 equal to 7
Using the second ratio:
(opp. 60)/(opp. 30) =
We found earlier that the side opposite 30 was 7. So
(opp. 60)/7 =
All we need to do now is multiply both sides by 7. On the left side the 7's cancel leaving:
opp. 60 =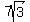 
The side opposite the 60 degree angle is the altitude so the length of the altitude is 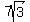(which is the same answer we got with the Pythagorean Theorem).
|
|
|
