Question 370334: Find all of the real zeros of the polynomial P(x)=2x^4-6x^3-52x^2-36x+56
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
A polynomial of degree 4, like P(x), can have up to 4 real roots. To find roots of a 4th degree polynomial them you often use factoring.
First we factor out the Greatest Common Factor, which is 2:

Now we try to factor 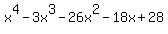 . This has too many terms for factoring by patterns and for trinomial factoring. And it has an odd number of terms so it doesn't seem that factoring by grouping will work. The only method left is trial and error of the possible rational roots. . This has too many terms for factoring by patterns and for trinomial factoring. And it has an odd number of terms so it doesn't seem that factoring by grouping will work. The only method left is trial and error of the possible rational roots.
The possible rational roots of 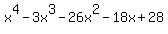 are all the fractions which can be formed by a factor of 28 over a factor of 1 (the leading coefficient), both positive and negative. So the possible rational roots for are all the fractions which can be formed by a factor of 28 over a factor of 1 (the leading coefficient), both positive and negative. So the possible rational roots for 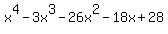 are 1/1. -1/1, 2/1, -2/1, 4/1, -4/1, 7/1, -7/1, 14/1, -14/1, 28/1, -28/1. are 1/1. -1/1, 2/1, -2/1, 4/1, -4/1, 7/1, -7/1, 14/1, -14/1, 28/1, -28/1.
The easiest way to determine if one of these is a root is with synthetic division. This is a trial and error method. I will omit all the rational roots I tried which did not work. I will just show the ones I found.
Using synthetic division to see if -2 is a root of 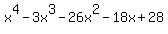 : :
-2 | 1 -3 -26 -18 28
---- -2 10 32 -28
---------------------
1 -5 -16 14 0
The remainder (in the bottom right corner) is zero. This means that (x - (-2)) or (x + 2) is a factor of 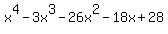 . The rest of the bottom line, 1 -5 -16 14, also tells you the other factor: . The rest of the bottom line, 1 -5 -16 14, also tells you the other factor: 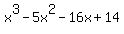 . So now we have: . So now we have:

Trying possible root of 7:
7 | 1 -5 -16 14
--- 7 14 -14
----------------
1 2 -2 0
The zero remainder means that (x-7) is a factor. So now we have:

Last of all we try to factor 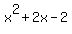 . This does not fit any pattern. It is a trinomial but it does not factor with trinomial factoring. It doesn't have enough terms for factoring by grouping and even factoring by trial and error of rational roots fails. But . This does not fit any pattern. It is a trinomial but it does not factor with trinomial factoring. It doesn't have enough terms for factoring by grouping and even factoring by trial and error of rational roots fails. But 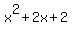 is a quadratic expression so we can use the Quadratic Formula: is a quadratic expression so we can use the Quadratic Formula:

which simplifies as follows:










So P(x) has two rational roots, -2 and 7, and two irrational roots, 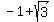 and and 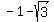 . .
|
|
|