Question 369834: log4((x^2)-9)-log4(x+3)= 3
x=?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
With an equation like this, where the variable is in the argument (or base) of a logarithm, you will often start the solution by transforming the equation into one of the following forms:
log(expression) = other-expression
or
log(expression) = log(other-expression)
With the non-log term of 3 on the right side the second form will be more difficult to achieve. So we will aim for the first form.
On the left side of your equation you have two logarithms of the same base with a "-" between them. And we want just a single logarithm. Fortunately there is a property of logarithms,  , which will allows us to do exactly what we want: Combine the two logarithms into one. Using this property on your equation we get:
We now have the first form. But before we proceed, I am going to reduce the fraction. The numerator is a difference of squares so it will factor according to that pattern:
The (x+3)'s cancel:
leaving
Now we can proceed. With the first form, the next step is to rewrite the equation in exponential form. In general,  is equivalent to  . Rewriting your equation in exponential form we get:
which simplifies to
x-3 = 64
Adding 3 to each side we get:
x = 67
Last of all we should check the solution. This is more than just a good idea when solving equations like this one. One must ensure that no solutions end up making an argument of a logarithm zero or negative. Zero or negative arguments of logarithms can happen even if you have not made any mistakes! This is why checking for this is not really an option with logarithmic equations like this.
Checking x = 67:
Since 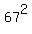 is much greater than 9 the first argument will definitely be positive. And the second argument is 70, also positive. So we can tell already that the arguments will both be positive. (If either or both arguments had turned out zero or negative, we would have to reject that "solution", even if it was the only "solution" we had found.)
We have done the part of the check which is required. The remainder of the check will tell us if we made any mistakes. You are welcome to complete the check on your own.
|
|
|
