SOLUTION: (25/4)^x+1=(2/5)^x-1

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: (25/4)^x+1=(2/5)^x-1      Log On


   

Question 367526: (25/4)^x+1=(2/5)^x-1
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
I'm assuming the equation is:
%2825%2F4%29%5E%28x%2B1%29=%282%2F5%29%5E%28x-1%29
If so, please enclose multiple term exponents, like these, in parentheses. Tutors are more likely to help with problems that are clear.

There are a couple of ways to solve this. I will show you both.

One solution requires that we recognize that 25/4 is the square of 5/2 and that 5/2 is the reciprocal of 2/5. So we'll start by replacing 25/4 with 5/2 squared:
%28%285%2F2%29%5E2%29%5E%28x%2B1%29=%282%2F5%29%5E%28x-1%29
The rule for exponents when raising a power to a power, like we are on the left side, is to multiply the exponents. This gives us:
%285%2F2%29%5E%282x%2B2%29=%282%2F5%29%5E%28x-1%29
Next I will take advantage of the fact that 5/2 and 2/5 are reciprocals. I'm going to multiply both sides by 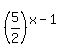%285%2F2%29%5E%28x-1%29. (You'll see why in a moment.)

On the left side, the rule for exponents tells us to add the exponents. On the right side, even though we do not know what x-1 is, we can tell that there are exactly the same number of (5/2)'s as there are (2/5)'s. So they will all pair up and cancel each other out leaving a 1 on the right side:
%285%2F2%29%5E%28%28x-1%29%2B%282x%2B2%29%29=1
The exponent on the left simplifies:
%285%2F2%29%5E%283x%2B1%29=1
Now the equation says that 5/2 to the 3x+1 power is 1. We can find x with some simple logic:
  • 1 to any power is 1.
  • -1 to any even power is also 1
  • For a power of any other number (except zero) to be 1, the exponent must be zero!

So for a power of 5/2 to be 1, the exponent must be zero!
3x+1 = 0
Solving this we get:
x = -1/3

Another approach would be to use logarithms and your calculator.
%2825%2F4%29%5E%28x%2B1%29=%282%2F5%29%5E%28x-1%29
We can start by finding the logarithm of each side. The base of the logarithm can be anything we like. But we should probably choose a base that your calculator "knows", like base 10 or base e (aka ln):
ln%28%2825%2F4%29%5E%28x%2B1%29%29=ln%28%282%2F5%29%5E%28x-1%29%29
Next we can use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponents of each argument out in front:
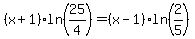
%28x%2B1%29%2Aln%2825%2F4%29=%28x-1%29%2Aln%282%2F5%29
Now we can get out our calculators and find the two logarithms:
%28x%2B1%29%2A1.8325814637483101=%28x-1%29%2A%28-0.9162907318741551%29
In spite of the decimals, we now have a fairly simple equation to solve. After using the Distributive Property we get:
1.8325814637483101x%2B1.8325814637483101=-0.9162907318741551x%2B+0.9162907318741551
Adding 0.9162907318741551x to each side we get:
2.7488721956224652x%2B1.8325814637483101=0.9162907318741551
Subtracting 1.8325814637483101 from each side we get:
2.7488721956224652x+=+-0.9162907318741551
And dividing both sides by 2.7488721956224652 we get:
x+=+-0.3333333333333333 which is a decimal which is extremely close to -1/3, the answer we got the with the other solution.

Note: I used ln here. You can use base 10 logarithms instead and you will end up with the same answer, even though the decimals you get from the base 10 logarithms are different!