SOLUTION: Please help me solve this equation: For which values of t is the curve {{{ x= t +lnt }}}, {{{ y= t-lnt }}} concave upward?

Algebra ->  Test -> SOLUTION: Please help me solve this equation: For which values of t is the curve {{{ x= t +lnt }}}, {{{ y= t-lnt }}} concave upward?       Log On


   

Question 366019: Please help me solve this equation:
For which values of t is the curve +x=+t+%2Blnt+, +y=+t-lnt+ concave upward?
Found 2 solutions by jsmallt9, robertb:
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
To determine the concavity we need the second derivative of y with respect to x. To find this we will find the second derivative of x with respect to t and the second derivative of y with respect to t. (Since the notation used in Calculus is not as standard as other parts of Math are and since Algebra.com's software does not make derivative notation easy, I am going to use more words than notation to explain what I'm doing.)

dx%2Fdt+=+1+%2B+1%2Ft
2nd derivative of x with respect to t = %28-1%29%2Ft%5E2

dy%2Fdt+=+1+-+1%2Ft
2nd derivative of y with respect to t = 1%2Ft%5E2

The second derivative of y with repect to x would be the ratio of the two second derivatives above:
2nd derivative of y with respect to x = (2nd derivative of y with respect to t)/(2nd derivative of x with respect to t)
or
2nd derivative of y with respect to x = %281%2Ft%5E2%29%2F%28%28-1%29%2Ft%5E2%29
which simmplifies to:
2nd derivative of y with respect to x = -1

Since there is no variable in the 2nd derivative of y with respect to x, the concavity is a constant -1. In short, concavity is negative everywhere. This means the curve is concave downward everywhere.

So the answer to "For which values of t is the curve ... concave upward?" is: There are no values of t where the curve is concave upward.

Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
The answer given by the other tutor is wrong. He claims that the 2nd derivative of y with respect to x is the same as the 2nd derivative of y wrt t OVER the 2nd derivative of x wrt t. THAT IS NOT TRUE!
Now d%5E2y%2Fdx%5E2+=+d%28dy%2Fdx%29%2Fdx+=%28+d%28dy%2Fdx%29%2Fdt%29%2F%28dx%2Fdt%29. Now dy%2Fdt+=+1-1%2Ft+=+%28t-1%29%2Ft, and dx%2Fdt+=+1%2B1%2Ft+=+%28t%2B1%29%2Ft. Hence dy%2Fdx+=+%28%28t-1%29%2Ft%29%2F%28%28t%2B1%29%2Ft%29+=+%28t-1%29%2F%28t%2B1%29. Hence
. (Used the quotient rule on the numerator derivative!)
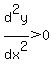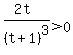For the parametric curve to be concave upward, d%5E2y%2Fdx%5E2+%3E0, or %282t%29%2F%28t%2B1%29%5E3+%3E+0. Solving this inequality, the critical numbers of the inequality are 0 and -1. Using the test numbers -2, -1/2, and 1, and checking for signs, the solution set is (-infinity, -1)U(0, infinity).