Question 36470: Determine the GCF of the following terms:
54x^5 y^7 z^3 , 72x^3 y^5 z^2 , 63x^4 y^3 z^9
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! The GCF for any terms is the product of all the factors that divide evenly into each of the terms. First find the largest number that divides into each of these numbers: 54, 72, and 63. Can you see that 9 divides evenly into each of these numbers? Yes! Is there any larger number that will do it? NO.
Now, look at the variables raised to different powers. You have x^5, x^3, and x^4. Can you see that x^3 divides into x^5, but x^5 does NOT divide into x^3? It turns out the the smaller powers of x, divide into the higher powers of x, so it is correct to choose the LOWEST POWER of each variable. The LOWEST power of x is x^3, the LOWEST POWER of y is y^3, and the LOWEST POWER of z is z^2. (By the way, I know it sounds funny to say the the GREATEST Common Factor is the LOWEST power of the variable, but it works that way.)
Final answer for the GCF: 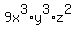
R^2 at SCC
|
|
|