|
Question 364482: Hi,
Im Struggeling with this question:
Vectors:
Show that vectors a = 2i-4j-k, b = 3i+2j-2k and c = 5i-2j-3k can form the sides of a triangle, find the length of each side and hence show that the triangle has a right angle. sketch the triangle of vectors, indicating their directions and the right angle,
Any help would be much appreciated?
Thanks
Scott
Found 3 solutions by Alan3354, isku, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Show that vectors a = 2i-4j-k, b = 3i+2j-2k and c = 5i-2j-3k can form the sides of a triangle, find the length of each side and hence show that the triangle has a right angle. sketch the triangle of vectors, indicating their directions and the right angle,
------------
Find the lengths:

a: 
a: s = sqrt(21)
b: s = sqrt(17)
c: s = sqrt(38)
---------------
c^2 is = a^2 + b^2, so it's a right triangle.
Answer by isku(1)   (Show Source): (Show Source):
You can put this solution on YOUR website! If two of three unit vectors are the same then they cannot form a triangle.
|a| = sqrt(4+16+1) = sqrt(21) <-length of a
|b| = sqrt(9+4+4 ) = sqrt(17) <-length of b
|c| = sqrt(25+4+9) = sqrt(38) <-length of c
â = a/|a| <-unit vector for a
= [ 2, -4, -1 ]/ sqrt( 21)
b̂ = b/|b| <-unit vector for b
= [ 3, 2, -2 ]/sqrt(17)
ĉ = c/|c| <-unit vector for c
= [ 5, -2, -3 ]/ sqrt(38)
If two vector are the same then the difference is zero
â - b̂ = [ 2, -4, -1 ]/ sqrt( 21) - [ 3, 2, -2 ]/sqrt(17) ≠ [0 0 0] <--they are not the same
â - ĉ = [ 2, -4, -1 ]/ sqrt( 21) - [ 5, -2, -3 ]/ sqrt(38) ≠ [0 0 0] <--they are not the same
b̂ - ĉ = [ 3, 2, -2 ]/sqrt(17) - [ 5, -2, -3 ]/ sqrt(38) ≠ [0 0 0] <--they are not the same
To control the assumption, let d = [ 2*2, -4*2, -1*2 ] i.e. 2*a
d̂ = [ 2*2, -4*2, -1*2 ] / sqrt( 16+64+4) = [ 2*2, -4*2, -1*2 ] / sqrt(84)
â - d̂ = [ 2, -4, -1 ]/ sqrt( 21) - [ 2*2, -4*2, -1*2 ] / sqrt(84) = [0 0 0] → â and d̂ are the same.
→ We cannot form a triangle by these three : a,b and d or a,c and d
Showing that it is right-angled
|a| = sqrt(4+16+1) = sqrt(21) length of a
|b| = sqrt(9+4+4 ) = sqrt(17) length of b
|c| = sqrt(25+4+9) = sqrt(38) length of c
Since |c|^2 = |a|^2 + |b|^2 ( using Pythagoras)
→ they forms a right-angled.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If three vectors "a", "b" and "c" are given (in 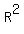 or in or in  , it does not matter),
then the necessary and sufficient condition for them to be the sides of a triangle / (to form a triangle) is the equality
a + b + c = 0.
You can EASILY check ON YOUR OWN that for the given vectors
a + b - c = 0.
It means that the vectors "a", "b" and "-c" form a triangle;
hence, the segments "a", "b" and "c" (if you forget about their directions) form a triangle. , it does not matter),
then the necessary and sufficient condition for them to be the sides of a triangle / (to form a triangle) is the equality
a + b + c = 0.
You can EASILY check ON YOUR OWN that for the given vectors
a + b - c = 0.
It means that the vectors "a", "b" and "-c" form a triangle;
hence, the segments "a", "b" and "c" (if you forget about their directions) form a triangle.
The second part of the proof, regarding right angle triangle, do in the same way as the other author did in his (or her) post.
---------------
See the lesson
- Sum of vectors that are coherently oriented sides of a convex closed polygon
in this site.
|
|
|
| |