|
Question 36358: 1.If α, b, g are the roots of the equation
x^3─7x^2 + x + 5 = 0
Find the equation whose roots are
α^2 + b^2, b^2 + g^2, g^2 + α^2.
2.Find all the fifth roots of (2+i).
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.If α, b, g are the roots of the equation
x^3─7x^2 + x + 5 = 0
Find the equation whose roots are
α^2 + b^2, b^2 + g^2, g^2 + α^2.
Sol: since α + b+ g= 7,
αb + bg+ gα = 1 and
αbg = - 5.
use α^2+ b^2 + g^2 = (α+b+g)^2 - 2(αb + bg+ gα) = 49 - 2 = 47.
(α^2 + b^2)(b^2 + g^2)+ (b^2 + g^2)(g^2 + α^2) + (g^2 + α^2)(α^2 + b^2)
= (47- g^2)(47- α^2) + (47- α^2)(47- b^2) + (47- b^2)(47- g^2)
= 3*47^2 - 47*2(α^2+ b^2 + g^2) + α^2 g^2 + α^2 b^2 + b^2 g^2
where α^2 g^2 + α^2 b^2 + b^2 g^2 = (αb + bg+ gα)^2 - 2αbg(α + b+ g)
= 1 + 10*7 = 71.
So, (α^2 + b^2)(b^2 + g^2)+ (b^2 + g^2)(g^2 + α^2) + (g^2 + α^2)(α^2 + b^2)
= 3*47^2 - 2*47^2 + 71 = 2280
And, (α^2 + b^2)(b^2 + g^2)(g^2+ α^2)
= (47- α^2)(47- g^2) (47- b^2)
= 47^3 - 47(α^2+ b^2 + g^2) + 47(α^2 b^2 + g^2b^2+ α^2g^2)- α^2 b^2 g^2
= 47^3 - 47^2 + 47*71- 25 = 104926
Hence, the required equation as:
x^3 - 47x^2 + 2280 x - 104926 = 0.
2.Find all the fifth roots of (2+i).
Use de Moevie(??) law;
2+i = r (cos t+ i sin t), where r = sqrt(2^2+1) = sqrt(5)
and t = ArcTan 1/2
the five 5th roots are r^(1/5) (cos 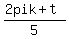 + +
i sin 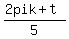 } }
for k = 0,1,2,3,4.
or 5^(1/10) (cos 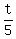 + i sin + i sin 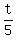 }, },
5^(1/10) (cos 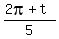 + i sin + i sin 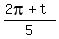 }, },
5^(1/10) (cos 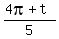 + i sin + i sin 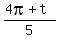 }, },
5^(1/10) (cos 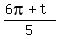 + i sin + i sin 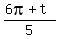 } , } ,
and
5^(1/10) (cos 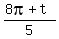 + i sin + i sin 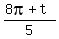 } }
Kenny
|
|
|
| |