SOLUTION: (1) find the x- intercepts of the graph of f(x) =2x^2-4x-4. (2) find all the vertical asymptotes for g(x) = x^2-4/x+2 (3) find {{{(f*g)}}}(x) if f(x) =3x-5 and g

Algebra ->  Graphs -> SOLUTION: (1) find the x- intercepts of the graph of f(x) =2x^2-4x-4. (2) find all the vertical asymptotes for g(x) = x^2-4/x+2 (3) find {{{(f*g)}}}(x) if f(x) =3x-5 and g      Log On


   

Question 36331: (1) find the x- intercepts of the graph of f(x) =2x^2-4x-4.


(2) find all the vertical asymptotes for g(x) = x^2-4/x+2



(3) find 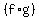%28f%2Ag%29(x) if f(x) =3x-5 and g(x)x^2+1
Answer by Nate(3500) About Me  (Show Source):
You can put this solution on YOUR website!
(1) find the x- intercepts of the graph of f(x) =2x^2-4x-4.
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 2x%5E2%2B-4x%2B-4+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-4%29%5E2-4%2A2%2A-4=48.

Discriminant d=48 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--4%2B-sqrt%28+48+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-4%29%2Bsqrt%28+48+%29%29%2F2%5C2+=+2.73205080756888
x%5B2%5D+=+%28-%28-4%29-sqrt%28+48+%29%29%2F2%5C2+=+-0.732050807568877

Quadratic expression 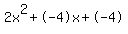2x%5E2%2B-4x%2B-4 can be factored:
2x%5E2%2B-4x%2B-4+=+2%28x-2.73205080756888%29%2A%28x--0.732050807568877%29
Again, the answer is: 2.73205080756888, -0.732050807568877. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+2%2Ax%5E2%2B-4%2Ax%2B-4+%29

(2) find all the vertical asymptotes for g(x)=(x^2-4)/(x+2)
g%28x%29=%28x%5E2-4%29%2F%28x%2B2%29
g%28x%29=%28%28x-2%29%28x%2B2%29%29%2F%28x%2B2%29
g%28x%29=%28x-2%29 where the vertical asymptote is the deleted denominator x%2B2
so x%2B2 is also expressed as: x=-2%29 that is the vertical asymptote
In the line below, the point as (-2,-4) doesn't exist....
Solved by pluggable solver: DESCRIBE a linear EQUATION: slope, intercepts, etc
Equation -1+x+%2B+1+y+=+-2 describes a sloping line. For any
equation ax+by+c = 0, slope is -a%2Fb+=+--1%2F1.
  • X intercept is found by setting y to 0: ax+by=c becomes ax=c. that means that x = c/a. -2/-1 = 2.
  • Y intercept is found by setting x to 0: the equation becomes by=c, and therefore y = c/b. Y intercept is -2/1 = -2.
  • Slope is --1/1 = 1.
  • Equation in slope-intercept form: y=1*x+-2.
graph%28+500%2C+500%2C+2-8%2C+2%2B8%2C+-2-8%2C+-2%2B8%2C+1%2Ax%2B-2+%29+

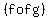(3) find %28f+of+g%29(x) if f(x) =3x-5 and g(x)x^2+1
Just plug in g(x) as 'x' for f(x)....
f%28x%29=3x-5
f%28x%29=3%28x%5E2%2B1%29-5
%28f+of+g%29%28x%29=3x%5E2-2