Question 362889: Due to melting, an ice sculpture loses one-half its weight every hour. After 8 hours, it weighs 5/16 of a pound. How much did it weigh in the beginning.
I did 5/16+8 and put the fraction into decimal form then added the two together and got 8.3125. Then its says 1/2 of the that is lost in weight. Now I multiplied the 8.3125 to .05(The decimal of 1/2) then got 4.15625. I dont know if that is correct or what and i used samdep instead of pemdas its pemdas backwards because it says to solve backwards using asmdep.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's say it weighed  to start. to start.
After  hour, it weighs hour, it weighs 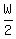
After  hours, it weighs hours, it weighs 
After  hours, it weighs hours, it weighs 
After  hours, it weighs hours, it weighs 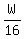
After  hours, it weighs hours, it weighs 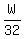
After  hours, it weighs hours, it weighs 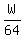
After  hours, it weighs hours, it weighs 
After  hours, it weighs hours, it weighs 
But you know that

So then,

 lbs lbs
.
.
.
You could also work it backwards,
After  hours it weighs hours it weighs  lb. lb.
After  hours it weighed hours it weighed  lb. lb.
After  hours it weighed hours it weighed  lb. lb.
After  hours it weighed hours it weighed  lb. lb.
After  hours it weighed hours it weighed  lb. lb.
After  hours it weighed hours it weighed  lb. lb.
After  hours it weighed hours it weighed  lb. lb.
After  hours it weighed hours it weighed  lb. lb.
After  hours it weighed hours it weighed  lb. lb.
|
|
|