|
Question 362638: list all rational zeros
use synthetic division to test the possible rational roots and find an actual root
x^3-2x^2-7x-4=0
Answer by shorty4aboo(8)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ok this is going to be a hard one to explain and i apologize now that i probably won't explain it good enough. Ok anyways......
Your problem is {{f(x)=x^3-2x^2-7x-4=0}}}
so with that we will list the possible zeros first.
In order to list these it will look like this.
P=+1,-1,+2,-2,+4,-4 [these are your factors of 4 the last # in your equ.]
Q=+1,-1 [these are your factors of 1 the first # in your equ.]
Then you put  to make your list so lets do that: to make your list so lets do that:
 , , , , This list converts to This list converts to
 , ,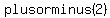 , ,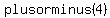 These are the only three numbers you will use within your synthetic division to find your zeros. Now when you go to synthetically divide if it is a true zero, the prob will end in zero. These are the only three numbers you will use within your synthetic division to find your zeros. Now when you go to synthetically divide if it is a true zero, the prob will end in zero.
so lets look at this:When you synthetically divide by
1 you get No zero because the remainder is -12 No zero because the remainder is -12
2 you get  No zero because the remainder is 18 No zero because the remainder is 18
4 you get  This is a zero because the remainder is 0 This is a zero because the remainder is 0
Lets rewrite the equ now with this zero in and we should be able to regulary factor out the last zero(s)[Don't forget to change your synthetic #'s sign].

Let us now factor 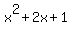 ...... This factors to ...... This factors to 
So the problem now looks like this:

Now that it is completely factored, lets find those zeros:
 would turn into would turn into  then this would turn into then this would turn into 
 would turn into would turn into  then this would turn into then this would turn into 
So your Zeros are : 4 and 1 (w/ multiplicty of 2)
Your # of zeros will always be either the same or lower than the power of your leading term. Out leading term in this equ. was  which means we could have 3 or less zeros and we have 3. Good Job! which means we could have 3 or less zeros and we have 3. Good Job!
Again I apologize because this is even complicated for me to understand and i wrote it. Yet try with what you know to make these numbers show up on your paper with pencil. If I just confused you so much more I sincerely apologize.
|
|
|
| |