Question 362462: 6x^2-5x-1/12x^2-11x+2 is less than 0
Found 2 solutions by stanbon, Fombitz:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 6x^2-5x-1/12x^2-11x+2 is less than 0
------
Factor:
[(6x+1)(x-1)]/[(3x-2)(4x-1)] < 0
------
Find the boundary values for the inequality
which are the solutions to the EQUALITY.
Those values are x = -1/6 and x = 1
Also take note of indeterminate values.
Those are x = 2/3 and x = 1/4
------
Draw a number line and plot the boundary values:
....-1/6....1/4....2/3....1....
---
To find the solutions for the inequality, test
a value from each of the three bounded intervals
in the inequality.
[(6x+1)(x-1)]/[(3x-2)(4x-1)] < 0
---
If x = -1 you get: (-*-)/(-*-) < 0; this is false
-----
If x = 0 you get: (+*-)/(-*-) < 0: true, so solutions in (-1/6,1/4)
-----
Do the same for x = 1/3 , for x = 5/6, and x = 1
=====================================================
Cheers,
Stan H.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! 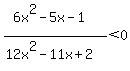
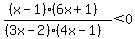
1, -1/6, 2/3, 1/4
Break up the number line into 5 regions using the critical points of the function.
Region 1:( , ,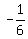 ) )
Region 2:(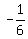 , , ) )
Region 3:( , , ) )
Region 4:( , , ) )
Region 5:( , , ) )
.
.
.
For each region, choose a point in the region (not an endpoint).
Test the inequality.
If the inequality is satisfied, the region is part of the solution region.
.
.
Region 1:
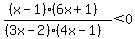
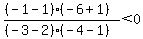
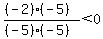
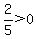
False, Region 1 is not part of the solution region.
.
.
Region 2:
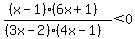
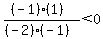

True, Region 2 is part of the solution region.
.
.
Region 3:
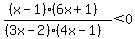
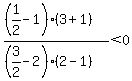
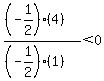
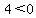
False, Region 3 is not part of the solution region.
.
.
Region 4:
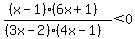
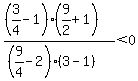
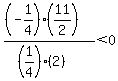
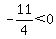
True, Region 4 is part of the solution region.
.
.
Region 5:
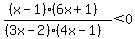
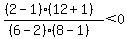
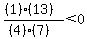
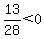
False, Region 5 is not part of the solution region.
.
.
Solution Region: (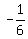 , , ) U ( ) U ( , , ) )
.
.
.
Graphical verification: Look for regions where the function is below the x-axis (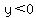 ) )
.
.
.

|
|
|