SOLUTION: I need to find the quotient and show all work {{{(64x^2 - 100y^2)/(8x + 10y)}}} This is what I have 64x^2 / 8x = 8x -100y^2 / 10y = -10y Is this correct? Can this

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I need to find the quotient and show all work {{{(64x^2 - 100y^2)/(8x + 10y)}}} This is what I have 64x^2 / 8x = 8x -100y^2 / 10y = -10y Is this correct? Can this       Log On


   

Question 362058: I need to find the quotient and show all work
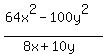
%2864x%5E2+-+100y%5E2%29%2F%288x+%2B+10y%29
This is what I have
64x^2 / 8x = 8x
-100y^2 / 10y = -10y
Is this correct? Can this be solved using long division. I tried that way but it doesn't come out right. I appreciate any help you can give me Thank you!
Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!

Yes, but not for the reason you state. Your process is flawed and you just got lucky with this one. Notice that the numerator of your fraction is the difference of two squares, so factor the numerator.



Then eliminate the common factor in the numerator and denominator.




John

My calculator said it, I believe it, that settles it
The Out Campaign: Scarlet Letter of Atheism

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
I need to find the quotient and show all work
%2864x%5E2+-+100y%5E2%29%2F%288x+%2B+10y%29
This is what I have
%2864x%5E2%29%2F%288x%29+=+8x
%28-100y%5E2%29%2F%2810y%29+=+-10y
Is this correct? 
No that's wrong.  You can't break up added or subtracted terms
in the numerator and denominator of a fraction the same way as 
you can break up factors in the numerator and denominator of a
fraction.

You can do this either of 2 ways:

1.  By factoring and canceling:

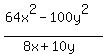%2864x%5E2+-+100y%5E2%29%2F%288x+%2B+10y%29

Factor 4 out of top
Factor 2 out of the bottom:

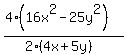%284%2816x%5E2+-+25y%5E2%29%29%2F%282%284x+%2B+5y%29%29

Cancel the 2 into the 4

 2
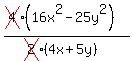
%28cross%284%29%2816x%5E2+-+25y%5E2%29%29%2F%28cross%282%29%284x+%2B+5y%29%29

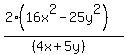%282%2816x%5E2+-+25y%5E2%29%29%2F%28%284x+%2B+5y%29%29

Factor the parenthetical expression in the top as the 
difference of two squares.

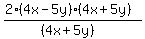%282%284x-5y%29%284x%2B5y%29%29%2F%28%284x%2B5y%29%29

Cancel the %284x%2B5y%29's

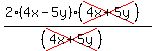%282%284x-5y%29%28cross%284x%2B5y%29%29%29%2F%28%28cross%284x%2B5y%29%29%29

All that's left is 2%284x-5y%29

And you can multiply that out as

          8x - 10y

--------------------------------

Can this be solved using long division. I tried that way but it doesn't come out right. I appreciate any help you can give me Thank you!

2.  Yes, it can also be done by long division:

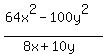%2864x%5E2+-+100y%5E2%29%2F%288x+%2B+10y%29

We insert a zero term in xy in the numerator:

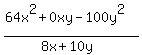%2864x%5E2+%2B0xy-+100y%5E2%29%2F%288x+%2B+10y%29

                  8x -  10y
8x + 10y)64x² +  0xy - 100y²
         64x² + 80xy 
               -80xy - 100y²  
               -80xy - 100y²

So the answer is the same

          8x - 10y
               
Edwin