SOLUTION: {{{9x^2-81y-12}}} {{{4a^2+24a+36}}} {{{36y^2-36}}} {{{4xy^2+12y+9}}} I need to know which of these is a perfect square trinomial

	
	
	


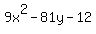
A perfect square trinomial must be a trinomial and a trinomial
has three terms, not just 2 so we can eliminate ,
which is only a binomial.

So it's between these three:

	
	


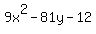
To be a perfect square trinomial, the first and last terms must
be perfect square monomials.

-12 is not a perfect square, so we can eliminate 

 is not a perfect square, so we can eliminate .

So the only possibility is 



To recognize a perfect square trinomial

1. There must be three terms.
2. The first and last terms must be positive perfect squares.
3. The middle term must be 2 times the product of the square roots
   of the first and last terms, and it can have either a + or a - sign.

  has three terms, so 1 is satisfied.

 is a positive perfect square, because it's 
 is a perfect square, because it's , so 2 is satisfied.

The square root of the first term  is .
The square root of the last term  is .
2 times their product is  is  and that's the
middle term with a positive sign.  So 3 is satisfied.

Edwin