Question 360337: In a diagram, a man is in a rowboat at point A, which is located 3 miles from point B, the closest point to A on a straight shoreline. The man needs to get to point C, on the same shoreline, 10 miles from B.
If the man travels on water at a rate of 1/2 miles per hour and travels on land at a rate of 3/2 miles per hour, where should he land the boat in order to arrive at point C in the SHORTEST amount of time?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a diagram, a man is in a rowboat at point A, which is located 3 miles from
point B, the closest point to A on a straight shoreline.
The man needs to get to point C, on the same shoreline, 10 miles from B.
If the man travels on water at a rate of 1/2 miles per hour and travels on land
at a rate of 3/2 miles per hour, where should he land the boat in order to
arrive at point C in the SHORTEST amount of time?
:
Let x = the distance from point B where the boat lands on the shore
then
(10-x) = the walking distance to point C
:
The rowing distance will be the hypotenuse, with sides x and 3
Rowing distance = 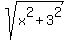
:
A time equation, Time = dist/speed
Use .5 mph for rowing speed and 1.5 mph for walking speed
:
Total time = rowing time + walking time
t = 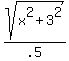 + + 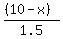
:
Graph the above equation, time on the y axis

Using a graphing calc, min: x=1.06, y=12.32 hrs
:
He should land the boat and walk 1.06 mi from A, for shortest travel time (12.32 hrs)
|
|
|