Question 360223: Find all zeros, both real and complex, of the polynomial function
f(x)= 2x^4-x^3+2x^2+19x-10
Answer by jrfrunner(365)   (Show Source):
You can put this solution on YOUR website! since the polynomial is of degree 4, there are 4 zeros or roots.
---
By descartes sign rule
f(+x) +-++- there are 3 or 1 positive real roots
f(-x) +++-- there is exactly 1 negative real root
since there is one negative real root, lets find it
==
looking at the constant 10, its factors are -+1,-+2,-+5,-+10 plus all the ones created by dividing these factors by -+1, -+2 from the leading constant 2
so the total possible reals are -+1/2,-+1,-+2,-+5/2,-+5,-+10
usually the roots will not be in the extreme so lest try -1.
f(-1)= so -1 no a root
--
try -2
f(-2)= so -2 is a root
--
Perform synthetic division to reduce the polynomial
yielding 
--
try another "potential root" from the list, now realizing that there is at least one positive real
--
try 1/2
through synthetic division you will find this works.
so now the functions is factored to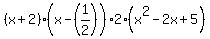 
--
using the quadratic equation on  we find that 1+2i and 1-2i are roots or zeros
--
So the four roots are -2, 1/2, 1+2i, 1-2i
|
|
|
