|
Question 359168: The road from Tedium to Excitement is uphill for 5 miles, level for 4 miles, and then downhill for 6 miles. John Mayer walks from Excitement to Tedium in 4 hours. Later he walks halfway from Tedium to Excitement and back again in 3 hours and 55 minutes. Finally he walks all the way to Excitement from Tedium in 3 hours and 52 minutes. What are his rates going uphill, downhill, and on level ground assuming that these rates remain constant?
Found 2 solutions by ankor@dixie-net.com, mathtutor19:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The road from Tedium to Excitement is uphill for 5 miles, level for 4 miles,
and then downhill for 6 miles.
John Mayer walks from Excitement to Tedium in 4 hours.
Later he walks halfway from Tedium to Excitement and back again in 3 hours and 55 minutes.
Finally he walks all the way to Excitement from Tedium in 3 hours and 52 minutes.
What are his rates going uphill, downhill, and on level ground assuming that
these rates remain constant?
:
Let u = uphill rate
Let f = flat rate
Let d = downhill rate
:
Write a time equation for each statement: Time = dist/rate
We are going to do it in minutes, change it to hrs later
:
"John Mayer walks from Excitement to Tedium in 4 hours."
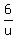 + + 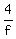 + + 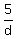 = 240 = 240
:
"he walks halfway from Tedium to Excitement and back again in 3 hours and 55 min."
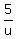 + + 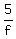 + + 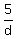 = 235 (halfway is 7.5 mi) = 235 (halfway is 7.5 mi)
:
"he walks all the way to Excitement from Tedium in 3 hours and 52 minutes."
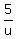 + + 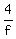 + + 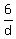 = 232 = 232
:
What are his rates going uphill, downhill, and on level ground assuming that these rates remain constant?
:
Use elimination on the 1st and 2nd equations
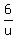 + + 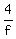 + + 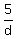 = 240 = 240
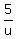 + + 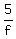 + + 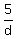 = 235 = 235
-----------------------------------------Subtraction eliminates d
 - - 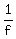 = 5 = 5
:
Multiply the 1st equation by 6 and the 3rd equation by 5
 + + 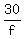 + + 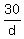 = 1410 = 1410
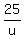 + +  + + 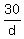 = 1160 = 1160
--------------------------------------------------Subtraction eliminates d again
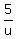 + + 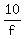 = 250 = 250
:
Multiply the 1st 2 unknown equation by 10, add to the above equation
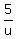 + + 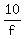 = 250 = 250
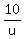 - -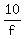 = 50 = 50
------------------addition eliminates f, find u
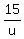 = 300 = 300
u = 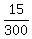
u =  miles per minute, that's miles per minute, that's  * 60 = 3 mph up hill * 60 = 3 mph up hill
:
Use the equation:  - - 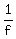 = 5 to find f,(were dealing mi/min here) = 5 to find f,(were dealing mi/min here)
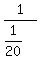 - - 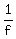 = 5 = 5
20 - 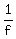 = 5 = 5
-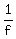 = 5 - 20 = 5 - 20
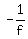 = -15 = -15
f = + mi/min, that's mi/min, that's  * 60 = 4 mph on the flat area * 60 = 4 mph on the flat area
:
We can use the 1st equation, using hrs, to find d
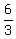 + + 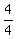 + + 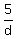 = 4 = 4
2 + 1 + 5/d = 4
5/d = 4 - 3
5/d = 1
d = 5 mph down hill
:
Summarize here
u = 3 mph uphill
f = 4 mph level
d = 5 mph down hill
:
:
See if this works int he original 3rd equation, using hrs
 + + 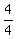 + + 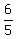 = 3 hr 52 min = 3 hr 52 min
1.67 + 1 + 1.2 = 3.87 hrs which is 3 hrs, .87*60 = 52.2 min, close enough
Answer by mathtutor19(8)   (Show Source): (Show Source):
You can put this solution on YOUR website! I agree with the other person's methods but the answers are:
uphill: 20
flat: 15
downhill:12
and it works perfectly in all the equations
the mistake was when you multiplied the first and third equations by 5. The flat rate for the first equation should by 20 not 30 (4*6=20)
|
|
|
| |