|
Question 358573: A suspension bridge with weight uniformly distributed along its length has twin towers that extend 85 meters above the road surface and are 1200 meters apart. The cables are parabolic in shape and are suspended from the tops of the towers. The cables touch the road surface at the center of the bridge. Find the height of the cables at a point 300 meters from the center. (Assume the road is level.
I can answer this question if I only knew how to turn the question into a function, which I do not. Help?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A suspension bridge with weight uniformly distributed along its length has twin
towers that extend 85 meters above the road surface and are 1200 meters apart.
The cables are parabolic in shape and are suspended from the tops of the towers.
The cables touch the road surface at the center of the bridge.
Find the height of the cables at a point 300 meters from the center. (Assume the road is level.
:
Find the equation for this:
Three coordinates:
0, 85; the vertical suspension point on the left
600, 0; the center point that touches the road (half the length of the bridge)
1200, 85; vertical suspension point on the right
:
Using: ax^2 + bx + c = y
:
0,85, we know c = 85
:
write two equation from coordinates;
x=600, y=0
(600^2)a + 600b + 85 = 0
360000a + 600b + 85 = 0
and
x=1200, y=85
(1200^2)a + 1200b + 85 = 85
2440000a + 1200b + 85 = 85
Multiply the 1st equation by 2, subtract from the 2nd equation
2440000a + 1200b + 85 = 85
720000a + 1200b + 170 = 0
------------------------------subtraction eliminates b, find a
720000a - 85 = 85
720000a = 85 + 85
720000a = 170
a = 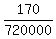
a = .0002361
find b, using the 1st equation:
.0002361(600^2) + 600b + 85 = 0
85 + 600b + 85 = 0
600b + 170 = 0
600b = -170
600b = 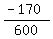
b = -.2833
:
The equation; y = .0002361x^2 - .2833x + 85
:
Looks something like this:

:
"Find the height of the cable at a point 300 meters from the center"
Now you can answer this question, I'm sure
|
|
|
| |