|
Question 358479: Please help me I'm stuck :(
Which is the equation of a line parallel to a line containing the points (-3, 1) and (6, 4) and passing throught the point (5, 2)?
Found 2 solutions by CharlesG2, Edwin McCravy:
Answer by CharlesG2(834)   (Show Source):
You can put this solution on YOUR website! Which is the equation of a line parallel to a line containing the points (-3, 1) and (6, 4) and passing throught the point (5, 2)?
slope-intercept form of a line is y = mx + b
where m is the slope,
and b is the y-intercept (vertical-intercept, or point (0,b))
m = slope = rise/run = (y2 - y1)/(x2 - x1)
m = (4 - 1)/(6 - -3) = 3/(6 + 3) = 3/9 = 1/3
parallel lines have the same slope
y = (1/3)x + b, solve for b by plugging in point (5,2)
2 = (1/3)(5) + b
2 = 5/3 + b
2 - 5/3 = b
1/3 = b (2 = 6/3)
y = (1/3)x + 1/3 (equation of line containing (5,2))
equation of line containing (-3,1):
1 = (1/3)(-3) + b
1 = -1 + b
2 = b
y = (1/3)x + 2
equation of line containing (6,4) will also be y = (1/3)x + 2:
4 = (1/3)(6) + b
4 = 6/3 + b
4 = 2 + b
2 = b
y = (1/3)x + 2
Answer by Edwin McCravy(20059)  (Show Source):
You can put this solution on YOUR website! Which is the equation of a line parallel to a line containing the points (-3, 1) and (6, 4) and passing throught the point (5, 2)?
First we'll draw the points that the first line goes through:
And then we'll draw that line.
We'll find the slope of that line using
      
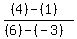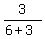The line parallel to that one must slope the same way, that is,
it must have the same slope.
Now we'll use the point-slope formula with (x1,y1) = (5,2)
 
 
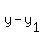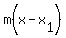
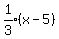Multiply both sides by 3:
 
 
 
 
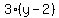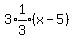
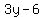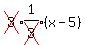
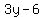
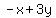
To check, we'll plot the point (5,2)
Then we'll get a couple more points
x | y
2 | 1
-1 | 0
Draw a line through those:
So the green line is parallel to the black line and it goes through (5,2).
Edwin
|
|
|
| |
