SOLUTION: Use the row echelon method to solve the system of three equations in three unknowns. 2x+y+z=9 -x-y+z=1 3x-y+z=9

Algebra ->  Matrices-and-determiminant -> SOLUTION: Use the row echelon method to solve the system of three equations in three unknowns. 2x+y+z=9 -x-y+z=1 3x-y+z=9       Log On


   

Question 358373: Use the row echelon method to solve the system of three equations in three unknowns.
2x+y+z=9
-x-y+z=1
3x-y+z=9
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!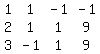
matrix%283%2C4%2C2%2C+1%2C1%2C9%2C-1%2C-1%2C1%2C1%2C3%2C-1%2C1%2C9%29~matrix%283%2C4%2C1%2C1%2C-1%2C-1%2C2%2C1%2C1%2C9%2C3%2C-1%2C1%2C9%29 Interchanging rows 1 and 2, and multiplying the new row 1 by -1.
~matrix%283%2C4%2C1%2C1%2C-1%2C-1%2C0%2C-1%2C3%2C11%2C0%2C-4%2C4%2C12%29, multiply row1 by -2, and multiply row1 -3.
~matrix%283%2C4%2C1%2C1%2C-1%2C-1%2C0%2C-1%2C3%2C11%2C0%2C0%2C2%2C8%29, add row2 to row3.
~matrix%283%2C4%2C1%2C1%2C-1%2C-1%2C0%2C1%2C-3%2C-11%2C0%2C0%2C1%2C4%29, multiply row2 and row3 by -1.
Thus z = 4, y - 3z = -11, x+y-z = -1.
y - 3*(4) = -11, y = -11+12 = 1,
x+y-z = -1. x+1-4 = -1, x-3=-1, x = 2.
Therefore x = 2, y = 1, and z = 4.