Question 357926: The sequence 3,a,b,c,768 is a geometric sequence. Find the values of a,b,and c.
Answer by Edwin McCravy(20063)   (Show Source):
You can put this solution on YOUR website! 3,a,b,c,768
Let the common ratio be r
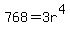Divide both sides by 3
Use the principle of even roots:
If r = +4, then
a = 3r = 3(+4) = 12
b = ar = 12(+4) = 48
c = br = 48(+4) = 192
and as a check:
768 = cr = 192(4) = 768 so that checks.
So one solution is a=12, b = 48, c = 192
---------------------------------------
If r = -4, then
a = 3r = 3(-4) = -12
b = ar = -12(-4) = 48
c = br = 48(-4) = -192
and as a check:
768 = cr = -192(-13) = 768,so that checks too.
So the other solution is a=-12, b = 48, c = -192
There are two solutions.
Edwin
|
|
|
