Question 35742: Determine the number of possible outcomes and please show work
How many ways can 6 items be selected for a gift basket from twelve possible items if the order of selection does not matter?
Thanks so much!
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a combination problem, since the order of selection does NOT matter. The number of ways of choosing 6 items from 12 is called a C(12, 6). There is a formula that a lot of people use, but I think it's easier to do it this way.
If it had been a permutation (in which the order DID matter), then it would be a P(12,6). With a P(12,6), start with 12*11*10*9*8*7 and multiply these 6 numbers together. If it had been P(12, 2), then the answer is 12*11. In other words the first number tells you where to start counting down, and the second number tells you how many numbers to multiply.
Now, the difference between a Combination and a Permutation is that with a Combination, you must multiply the same numbers as for a permutation, but divide by the factorial of the second number. Here are some examples of combinations:
C(5,2) = 
C(6,2) = 
C(12,2) = 
C(5,3) = 
Now here at last is YOUR question:
C(12,6)= 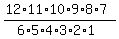
Got a calculator??? I got 924 for the answer. By the way, most of your calculators, even a $15 TI 30 will do this for you, so you don't have to understand this lesson!!
R^2 at SCC
|
|
|