SOLUTION: Simplify. Assume that no radicands were formed by raising negaitve quantaties to even powers. {{{sqrt(128a^2b^4)/sqrt(16ab)}}}

Algebra ->  Radicals -> SOLUTION: Simplify. Assume that no radicands were formed by raising negaitve quantaties to even powers. {{{sqrt(128a^2b^4)/sqrt(16ab)}}}      Log On


   

Question 35734: Simplify. Assume that no radicands were formed by raising negaitve quantaties to even powers.

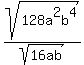
sqrt%28128a%5E2b%5E4%29%2Fsqrt%2816ab%29
Answer by rapaljer(4671) About Me  (Show Source):
You can put this solution on YOUR website!
Congratulations on writing your own equation box!! First off, you can make a single radical out of this
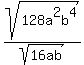
sqrt%28128a%5E2b%5E4%29%2Fsqrt%2816ab%29
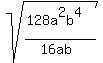
sqrt%28%28128a%5E2b%5E4%29%2F%2816ab%29%29

Next, reduce the fraction inside the radical. Notice that 16 goes into 128 about 8 times, and the "a" and "b" divide out leaving an 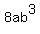8ab%5E3 in the numerator.

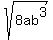
+sqrt%288ab%5E3%29

Now, sort this out and place in TWO separate square roots, where you will put all the PERFECT SQUARE factors in the first radical, and all the left over factors in the second radical. Notice that 8 has a perfect square that divides into it, which would be 4 (and the left over factor is 2), and b%5E2 is a perfect square, which leaves factors of "a" and "b" left over.

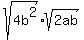
sqrt%284b%5E2%29%2A+sqrt%282ab%29+

Take the square root of the first radical, and leave the second one alone:
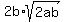
2b%2Asqrt%282ab%29+

R^2 at SCC