Question 357331: A plane needs to fly to a town located 200 km away in the direction 50 degrees east of north. There is westerly wind blowing at 60 km/h.
Determine the plane's airspeed and the direction in the degrees east of north, so it can fly directly to the town in 1/2 hour.
Help me please with the question.
Thank you!
Found 2 solutions by Alan3354, Theo:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A plane needs to fly to a town located 200 km away in the direction 50 degrees east of north. There is westerly wind blowing at 60 km/h.
Determine the plane's airspeed and the direction in the degrees east of north, so it can fly directly to the town in 1/2 hour.
--------------
The groundspeed has to be 400 km/hr (200 km/0.45 hr)
The wind is 60 from the west.
The angle between the flight path and the wind direction is 40º where they meet at the town.
This makes a triangle with sides meeting at the town of 400 and 60 with the angle between them of 40º.
Use the Cosine Law to find the 3rd side, with is the plane's airspeed.


airspeed = 356.13 km/hr
---------------------
Use the Law of Sines to find the heading of the plane:
356.13/sin(40) = 60/sin(B)
sin(B) = 60*sin(40)/356.13 = 0.10829
B = 6.217º
Heading = 50 - B = 43.8º
or 43.8 East of North
--------------------
PS Wind info is always given as the direction it's from.
A "westerly wind" of 10 knots would be given as "winds 270 at 10"
West is 270, and 10 is the windspeed in knots.
--------------------------
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe this is the correct interpretation of your problem.
Best for you to confirm with another source as well to be absolutely sure.
plane is traveling 50 degrees east of north.
that puts it at 40 degrees north of east.
distance is 200 km
in order for the plane to reach its destination without the effect of the wind, it would have to travel at 200/.5 = 400 kmph.
400 kmph for 1/2 hour means a distance of 200 km has been flown.
the length of the vector for the speed of the airplane would be 400 in the direction of 40 degrees north of east (same as 50 degrees east of north)
there is an x component to the speed of the airplane and a y component to the speed of the airplane.
the x component is equal to 400 * cos(40) = 306.4177772 kmph.
the y component is equal to 400 * sin(40) = 257.1150439 kmph
the plane is traveling 257 kmph in a northerly direction and 306 kmph in an easterly direction to get a net speed of 400 kmph in a north easterly direction.
the wind is traveling in a westerly direction at 60 kmph.
this has an impact on the speed of the airplane in an easterly direction.
the net speed of the airplane in the easterly direction will be 306... - 60 = 246.4177772 kmph.
in order for the plane to have a net speed of 306 in the easterly direction, it has to travel at 366.4177772 kmph in an easterly direction because 366.4177772 - 60 = 306.41777772.
the speed at which it travels in a northerly direction will be the same.
to counteract the effects of the wind, the plane has to travel at 366.4177772 kmph in an easterly direction and 257.1150439 kmph in a northerly direction.
the angle at which the plane needs to travel is determined by the arc-tan of y/x which equals 257... / 366... = 35.0573065 degrees north of east.
that's equivalent to 54.9426935 degrees east of north.
the speed that the plane will have to travel in the direction of that angle would have to be the square root of x^2 + y^2 which would be equal to the square root of ( 257... squared + 366... squared).
that comes out to be 447.6272258 kmph in the direction of 54.9426935 degrees east of north, or in the direction of 35.0573065 degrees north of east.
A picture is shown below:
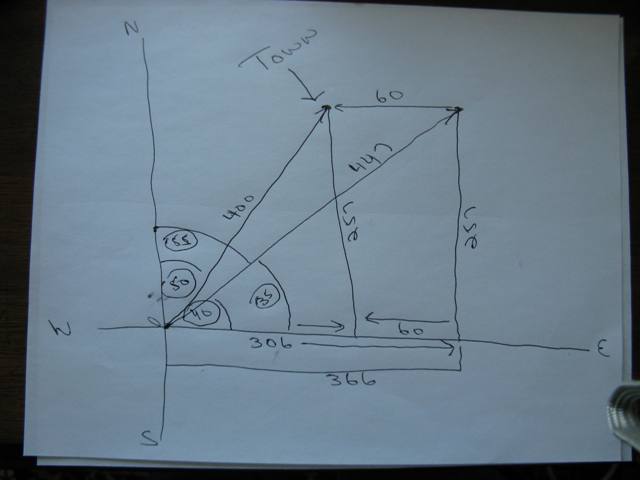
You want to get to the town, but because of the wind, you have to shoot for a point 30 km east of the town. The wind will push you back and you will arrive at the town. In order to do that, you need to travel at 447 kmph at 35 degrees north of east rather than 400 kmph at 40 degrees north of east.
|
|
|