Question 356762: An unidentified object moves along the s-axis, with displacement s = s(t) (meters), velocity v = v(t) (m/sec), and acceleration a = a(t) (m/sē). It so happens that the velocity and displacement are related by the equation v = sqrt(8s+16). Moreover, at the instant t = 0, the object is observed at s = 6. A) Show that a is constant, and show its value. B) Graph v as a function of s. C) Graph v as a function of t.
Answer by Jk22(389)   (Show Source): (Show Source):
You can put this solution on YOUR website! v=Sqrt(8s+16),
A) a=dv/dt=1/2*1/Sqrt(8s+16)*8v=4v/Sqrt(8s+16)=4v/v=4 (m/s^2)
(Other way : v^2*m/2=Kinetic Energy=m*(4s+8)
Potential Energy = Constant - Kinetic Energy = Const - 4ms -8m
Force = - d(Potential Energy)/ds = 4m = m*a => a=4 m/s^2)
B) v=Sqrt(8s+16)
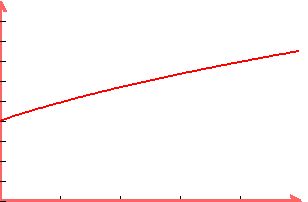
with v=ds/dt we get a differential equation :
ds/Sqrt(8s+16)=dt=ds/(2Sqrt(2s+4))
Integration gives :
t+C=1/2*Sqrt(2s+4),
indeed d(t+C)=dt, C is a constant
1/2*d(Sqrt(2s+4))=1/2*1/(2Sqrt(2s+4))*2=1/(2*Sqrt(2s+4))=1/Sqrt(8s+16)
s(t=0)=6 : at t=0, s=6, in the equation : C=1/2*Sqrt(12+4)=1/2*Sqrt(16)=2
the function displacement towards time is :
s(t)=1/2*(2t+4)^2-4
=1/2(4t^2+16*t+16)-16
=2t^2+8t-8 (m)
C) the velocity is : v(t)=ds/dt=
=4t+8 (m/s)
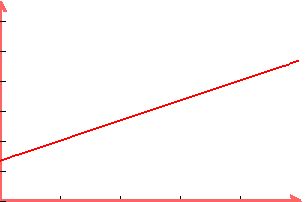
Verification : acceleration is : a(t)=dv/dt=4 (m/s^2)
|
|
|