Question 356729: What is a subspace ? How do you prove that it is a subspace ?
I know that it is a straight line or plane that passes through the origin.
But the proof of a subspace of 3 rules seems too basic.
It almost allows all vectors to be subspaces. I have not seen a vector that is not a subspace yet.
the rules are something like multiply by 0
addition of u and v scalars
multiplication by scalars.
My assignment question reads
W is the space of all vectors of the form (x, y, x-y) Find out if W is a subspace. JUstify your answer.
I need the answer put in basic english, with as much detail as possible. The question somehow is worth 10% of assignment, and to me it seems to basic. I just have problem with the wording.
Can anyone help with expressing this answer in clear English.
Thank You
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! Assuming addition of vectors and scalar multiplication in  , two conditions had to be met for a subset to be a subspace:
i) If u and v are vectors in W, then u + v is in W, and
ii) If u is in W, and c is a a scalar, then c*u is in W.
For the question above,
i) (x, y, x-y)+(z, w, z-w) = (x+z, y+w, x-y+z-w) = (x+z, y+w, (x+z)-(y+w)),
ii)c*(x, y, x-y) = (cx, cy, c(x-y)) = (cx, cy, cx-cy).
Therefore W is a subspace of  .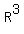
|
|
|
