Question 356159: I need help with this proof: Let x1....xk be linearly independent vectors in R^n, and let A be a nonsingular nXn matrix. Define yi = Axi for i = 1,...k. show that y1,.... yk are linearly independent. Thanks!
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider the linear combination:
(a1)(y1)+(a2)(y2)+(a3)(y3)+....+(a(n-1))(y(n-1))+(an)(yn)= 0, a1, a2, a3,...an are scalar coefficients.
For the purpose of contradiction, suppose that {y1, y2, y3,...,yn} is a linearly dependent set. Therefore not all of a1, a2, a3, ...an are equal to zero, by definition. Since A is nonsingular, 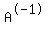 exists. exists.
Now
(a1)(y1)+(a2)(y2)+(a3)(y3)+....+(a(n-1))(y(n-1))+(an)(yn)=
(a1)(Ax1)+(a2)(Ax2)+(a3)(Ax3)+....+(a(n-1))(Ax(n-1))+(an)(Axn)=
A((a1)(x1)+(a2)(x2)+(a3)(x3)+....+(a(n-1))(x(n-1))+(an)(xn))= 0.
Since A is nonsingular, this means that 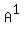 exists. Left-multiply the equation exists. Left-multiply the equation
A((a1)(x1)+(a2)(x2)+(a3)(x3)+....+(a(n-1))(x(n-1))+(an)(xn))= 0
by 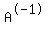 . This means that . This means that
(a1)(x1)+(a2)(x2)+(a3)(x3)+....+(a(n-1))(x(n-1))+(an)(xn)= 0,and
not all a1, a2, a3, ...an are equal to zero, CONTRADICTION, because {x1, x2, x3, ...xn} is a linearly independent set. Therefore
{y1, y2, y3,...,yn} has to be a linearly independent set.
|
|
|