Let the 1st traveler's rate be x mph
Let the 2nd traveler's rate be y mph
Let's take a look at the moment when they met, which was 9:05.
At 9:05 the 1st traveler, who started at 5AM, had been traveling for
4 hours and 5 minutes, or 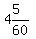 hours or
hours or 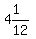 hours or
hours or 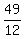 hours.
At rate x mph, he had traveled
hours.
At rate x mph, he had traveled 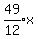 or
or 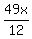 miles.
At 9:05 the 2nd traveler, who started at 7AM, had been traveling for
2 hours and 5 minutes, or
miles.
At 9:05 the 2nd traveler, who started at 7AM, had been traveling for
2 hours and 5 minutes, or 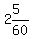 hours or
hours or 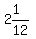 hours or
hours or 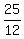 hours.
At rate y mph, he had traveled
hours.
At rate y mph, he had traveled 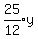 or
or 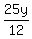 miles.
When they met at 9:05, each had the same number of miles yet to go that
the other had already been. That is, the 1st traveler had
miles.
When they met at 9:05, each had the same number of miles yet to go that
the other had already been. That is, the 1st traveler had 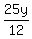 miles yet to go and the 2nd traveler had
miles yet to go and the 2nd traveler had 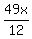 miles yet to go.
We are told that they arrived at the same time. So we will calculate each
traveler's time after 9:05 and set them equal.
Since
miles yet to go.
We are told that they arrived at the same time. So we will calculate each
traveler's time after 9:05 and set them equal.
Since  , the 1st traveler's time was his distance yet
to go,
, the 1st traveler's time was his distance yet
to go, 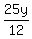 , divided by his rate x, or
, divided by his rate x, or 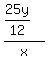 or
or  or
or  hours till he
reached town B.
Also the 2nd traveler's time was his distance yet to go,
hours till he
reached town B.
Also the 2nd traveler's time was his distance yet to go, 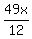 , divided
by his rate y, or
, divided
by his rate y, or  or
or 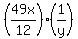 or
or 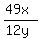 hours till he reached town A.
Since they arrived at their respective destinations at the same time, we set
these times equal:
hours till he reached town A.
Since they arrived at their respective destinations at the same time, we set
these times equal:


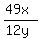 Multiplying both sides by 12 eliminates the 12's from the denominators:
Multiplying both sides by 12 eliminates the 12's from the denominators:
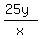

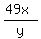 Cross multiplying:
Cross multiplying:
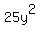

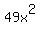 Taking positive square roots of both sides
Taking positive square roots of both sides
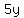

 Dividing both sides by 5x
Dividing both sides by 5x


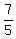 The 1st traveler's time to reach his destination after 9:05 was
The 1st traveler's time to reach his destination after 9:05 was
 which equals
which equals 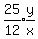 which equals
which equals

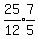

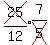

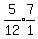

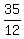

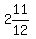

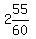 or 2 hours and 55 minutes after 9:05.
So the 1st traveler reached his destination at 12 noon.
It isn't necessary, but, as a check, let's see if the 2nd traveler also reached
his destination at 12 noon.
The 2nd traveler's time to reach his destination after 9:05 was
or 2 hours and 55 minutes after 9:05.
So the 1st traveler reached his destination at 12 noon.
It isn't necessary, but, as a check, let's see if the 2nd traveler also reached
his destination at 12 noon.
The 2nd traveler's time to reach his destination after 9:05 was
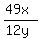 which equals
which equals 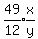 which equals
which equals

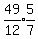

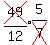

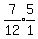

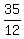

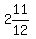

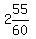 or 2 hours and 55 minutes after 9:05.
So the 2nd traveler also reached his destination at 12 noon.
So the 1st traveler started at 5AM and arrived at noon, so his time was 7 hours.
The 2nd traveler started at 7AM and arrived at noon, so his time was 5 hours.
[Notice that this problem is independent of their speeds and the distance they
traveled.]
Edwin
or 2 hours and 55 minutes after 9:05.
So the 2nd traveler also reached his destination at 12 noon.
So the 1st traveler started at 5AM and arrived at noon, so his time was 7 hours.
The 2nd traveler started at 7AM and arrived at noon, so his time was 5 hours.
[Notice that this problem is independent of their speeds and the distance they
traveled.]
Edwin