SOLUTION: how to find the range for the measure of the third side of a triangle given the measures of two sides 8 and 13

Let the third side be x.

Then we use the fact that the sum of any two sides of a triangle must be
greater than the other side.

So if the sides are 8, 13 and x then we must have all three of these:






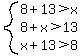
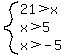The third one  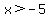is automatically taken care of by 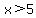, so we can
ignore that one and just have



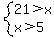which can be written as  5 < x < 21

So the range for the measure of the third side x is {x| 5 < x < 21} in set
builder notation  or (5,21) in interval notation.

-----

There is an easier way if you learn it.

Given the measures of two sides of a triangle, the measure of the third side is
between their difference (in absolute value) and their sum, exclusive of each.

So using that rule 13-8 < x < 13+8
                      5 < x < 21, or (5,21)

Edwin