|
Question 355705: Regarding Products of Sums and Differences
Multiply and simplify (3xy^2+4y)(-3xy^2+4y)
1) Please show me the steps to solving this. I have tried numberous times and do not get the answer the book shows.
2)Why is commutative law used? How should I know when to use it? Why are they switched? How should I know on my own when to switch them? The book shows the first step goes to (4y+3xy^2) (4y-3xy^2). I do not understand that at all.
I appreciate any help.
Jill
Found 2 solutions by mananth, Theo:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! (4y+3xy^2) (4y-3xy^2)
to put in simple terms you have to multiply each term in one bracket with the other terms in the second bracket.
...
4y(4y-3xy^2)+3xy^2(4y-3xy^2)
now you have to multiply the term outside the bracket with the terms in the bracket.( distributive law)
...
4y*4y-4y*3xy^2+3xy^2*4y-3xy^2*3xy^2
16y^2-12xy^3+12xy^3-9x^2y^4
16y^2-9x^2y^4
..
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! Multiply and simplify (3xy^2+4y)(-3xy^2+4y)
The distributive rule is:
a * (b + c) = (a*b) + (a*c)
The more generalized distributive rule is:
(a+b) + (c + d) = (a*c) + (a*d) + (b*c) + (b*d)
you can theoretically expand this as many times as you want, i.e. you can also get:
(a + b + c) * (d + e + f) = (a*d) + (a*e) + (a*f) + (b*d) + (b*e) + (b*f) + (c*d) + (c*e) + c*f)
An easy way to see this is to give each variable a number.
Let a = 1, b = 2, c = 3, d = 4, e = 5, f = 6)
You can see that (a + b + c) = 6 and (d + e + f) = 15 and 6 * 15 = 90
Start with (1 + 2 + 3) * (4 + 5 + 6) and distribute them according to the laws of distribution.
You will get:
(1*4) + (1*5) + (1*6) + (2*4) + (2*5) + (2*6) + (3*4) + (3*5) + (3*6)
simplify this to get:
4 + 5 + 6 + 8 + 10 + 12 + 12 + 15 + 18
add them all up together to get 90.
The distribution laws work.
The commutative laws are:
a*b = b*a
they can be extended to say:
a*b*c = a*c*b = b*a*c = b*c*a = c*a*b = c*b*a
Again, put it into number and you can see that they work.
let a = 1, b = 2, c = 3
you can see that 1*2*3 = 6 and 1*3*2 = 6 and 2*1*3 = 6 and 2*3*1 = 6, etc.
The commutative laws work.
The associative laws state that:
a*(b*c) = (a*b)*c
Again, you can see that this works by substituting number for letters.
Let a = 1, b = 2, c = 3, and you get:
1*(2*3) = 1*6 = 6
(1*2)*3) = 2*3 = 6
etc.
The associative laws work.
Now to your problem.
Your problem is:
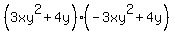
This can be re-written as:
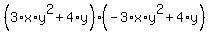
Use the distributive law to break these out.
you get:
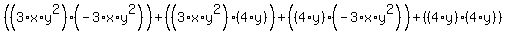
To simplify within each set of outer set of parentheses, you would use the associative law.
Example:
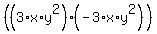
The associative law say that you can re-write this as:
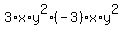
The commutative law says that you can re-write this as:
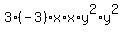
The associative law says that you can regroup them as:
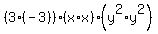
You then simplify by performing the operations indicated starting from the inner set of parentheses and working out.
The expression becomes:
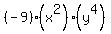 which can be re-written as: which can be re-written as:
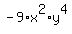
The associative law allowed you to do that.
You do the same with all the other multiplications within each set of parentheses to get:
 becomes: becomes:


you now combine like terms to get:
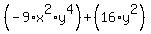
those 2 middle terms canceled out.
This can also be written as:
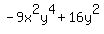
To convince yourself that you did it right, you can substitute numbers for letters and see if you get the same answer with the original equation and the final equation.
let x = 2 and y = 3.
the final equation becomes -9*4*81 + 16*9 = -2916 + 144 = -2772
the original equation of (3xy^2+4y)(-3xy^2+4y) becomes:
(3*2*9 + 4*3) * (-3*2*9 + 4*3) which becomes:
66 * -42 which becomes -2771
We got the same answer so we must have done it right.
The test is not fool proof but most of the time it works.
If you're in doubt, then pick some other numbers and go through the exercise again.
If it comes up good 2 or 3 times when you choose random numbers, then odds are the solution is good.
|
|
|
| |