SOLUTION: Please help me solve this equation: Solve the following system of equations by determining the inverse of the matrix of coefficients and then using matrix multiplication. x+

I will assume you already know how to find the inverse
of a matrix, and how to multiply two matrices. If you don't, 
post again asking how.  Each of those is is a separate topic.

First we form three matrices, A, X, and B.

1. Matrix A is the 3x3 coefficient matrix A, which consists 
of just the three columns of x, y, and z coefficients. in 
that order, but does not contain the column of constants.

. 

2. Matrix X is the 3x1 matrix of variables 

3. Matrix B is the 3x1 matrix, whose only column is the
column of constants: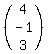 

Next we form the matrix equation:

       

or



To solve the equation

       

we left-multiply both sides by 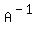, the inverse of .

 

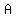Then since the associatitive principle holds for matrix multiplication,
(even though the commutative principle DOES NOT!!!), we can move
the parentheses on the left around the first two matrix factors:



Now since , where I is the identity matrix, the
above becomes:



and by the identity property:



Performing these operations with the actual matrices we have
the equation 




Next we form the inverse of A, which is written A-1.



Remember I assume you know where I got this inverse.  It is a whole separate
problem on how to find it.  If you don't know how, post again asking how.

Then we indicate the left multiplication of both sides by
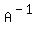 to get the equation :



Next we use the associative principle to move the parentheses so that
they are around the first two factors to get the equation :



Now we perform the actual multiplications and we get the equation :



Then when we multiply the identity matrix  by the column matrix of
variables, we just get the matrix of variables, or the 
equation 



So , , and 

Edwin