|
Question 354941: ^5sqrt(96x^5)
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Simplifying radicals involves:- Eliminating any fractions within a radical
- Eliminating any radicals in the denominator of a fraction
- "Reducing" the radical by factoring out perfect powers of the type of root.
Since your expression (pronounced "the 5th root of 96 x to the 5th power")
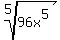
has no fractions, we can skip the first two parts of simplifying. Now we just look for perfect power factors. Since your expression is a 5th root, then we look for factors which are perfect powers of 5. Obviously 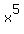 is a power of 5. But we also look for perfect powers of 5 in the 96. Since  and since 96 = 32*3, there is another power of 5 factor, 32, in your expression. Rewriting your expression with its radicand factored we get:
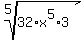
(Since multiplication is Commutative, the order of the factors is not important. I like to order the factors with the perfect power factors first and other factors, if any, at the end.)
Now we can use a basic property of all radicals,  , to separate each factor into its own personal radical:
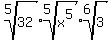
The 5th roots of the power of 5 factors are easy to find:
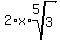
or
|
|
|
| |
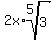
