SOLUTION: how to solve for x: 3times 7^x-1=5^2x+1

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: how to solve for x: 3times 7^x-1=5^2x+1      Log On


   

Question 354539: how to solve for x: 3times 7^x-1=5^2x+1
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
If your problem is:
3%2A7%5E%28x-1%29=5%5E%282x%2B1%29
then please use parentheses around multiple term exponents. The way you posted the question meant:
3%2A7%5Ex-1=5%5E2x%2B1
which is a very different (and more difficult) problem. Tutors are more likely to answer your questions if the problems are clear.

I will solve the easier problem, guessing that is what you really meant:
3%2A7%5E%28x-1%29=5%5E%282x%2B1%29
To solve an equation where the variable is in one ore more exponents, one usually uses logarithms (for reasons that will become clear later). A logarithm of any base may be used. But the answer will be in simpler form if you choose a base which matches the base of one of the exponents. So we will use either base 7 or base 5. I'm going to choose base 5. So we will find the base 5 logarithm of each side:
log%285%2C+%283%2A7%5E%28x-1%29%29%29=+log%285%2C+%285%5E%282x%2B1%29%29%29
Now we can start using properties of logarithms to simplify this expression. First, I'll use the property, log%28a%2C+%28p%2Aq%29%29+=+log%28a%2C+%28p%29%29+%2B+log%28a%2C+%28q%29%29, to separate the two factors in the first log:

Next, I'll use another proerty, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponents in the arguments out in front (as coefficients). This ability to move exponents like this is the reason we use logarithms for these problems. The property allows us to move an exponent (which has a variable in it) out in front where "we can get at it" with regular Algebra. Using this property on your expression we get:
log%285%2C+%283%29%29+%2B+%28x-1%29log%285%2C+%287%29%29=+%282x%2B1%29log%285%2C+%285%29%29
By definition, log%285%2C+%285%29%29+=+1. (This is why choosing base 5 (or 7) logarithms results in a simpler solution.) So the expression simplifies to:
log%285%2C+%283%29%29+%2B+%28x-1%29log%285%2C+%287%29%29=+2x%2B1
Now that the variables are accessible, we can start solving for x. First we'll use the Distributive Property to multiply on the left side:
log%285%2C+%283%29%29+%2B+x%2Alog%285%2C+%287%29%29+-+log%285%2C+%287%29%29+=+2x%2B1
Next we'll gather the x terms on ones side and the other terms on the other side:
log%285%2C+%283%29%29+-+log%285%2C+%287%29%29+-+1+=+2x+-+x%2Alog%285%2C+%287%29%29
Next we'll factor out x on the right side:
log%285%2C+%283%29%29+-+log%285%2C+%287%29%29+-+1+=+x%282+-+log%285%2C+%287%29%29%29
And then we'll divide both sides by 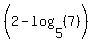%282+-+log%285%2C+%287%29%29%29

This may be an acceptable answer. Or you could use yet another property of logarithms, log%28a%2C+%28p%2Fq%29%29+=+log%28a%2C+%28p%29%29+-+log%28a%2C+%28q%29%29, (from right to left) to combine the two logarithms in the numerator:
%28log%285%2C+%283%2F7%29%29+-+1%29%2F%282+-+log%285%2C+%287%29%29%29+=+x
Either of these last two expresssions are exact expressions for the solution to the equation.

If you need/want a decimal approximation for the answer, then either use base 10 (or base e) logarithms from the start (instead of base 5) or use the base conversion formula to convert the base 5 logs in the answer above into base 10 (or base e) logarithms.