SOLUTION: write the absolute value function without absolute value sign g(x)= 2[x+1] + 5[1+5] if x< -5

Algebra ->  Absolute-value -> SOLUTION: write the absolute value function without absolute value sign g(x)= 2[x+1] + 5[1+5] if x< -5       Log On


   

Question 353575: write the absolute value function without absolute value sign g(x)= 2[x+1] + 5[1+5] if x< -5
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
I'm going to assume that
g%28x%29=+2abs%28x%2B1%29+%2B+5%2Aabs%28x%2B5%29

In order to solve this problem, we need to understand the basics of absolute values.
  • When a number is positive or zero, its absolute value is the same as the number itself. For example, abs%2813%29+=+13. Saying this "in Math":
    abs%28a%29+=+a if a+%3E=+0
  • When a number is negative, its absolute value is the negative of itself. For example, abs%28-45%29+=+-%28-45%29+=+45. Saying this "in Math":
    abs%28a%29+=+-a if a+%3C+0

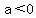
Your function has two absolute values. And, if x < -5, both expressions inside the absolute values, (x+1) and (x+5), will be negative! And if the expression inside the absolute value is negative, its absolute value is the negative of itself. So abs%28x%2B1%29+=+-%28x%2B1%29+=+-x+-1 and abs%28x%2B5%29+=+-%28x%2B5%29+=+-x+-5. This makes g(x):
g%28x%29+=+2%28-x-1%29+%2B5%28-x-5%29
Simplifying we get:
g%28x%29+=+-2x-2+%2B+%28-5x%29+%2B+%28-25%29
g%28x%29+=+-7x+-+27
(Note: Remember that g(x) equals the above equation only if x < -5.